Insights into fluidic endogenous magnetism and magnetic monopoles from a liquid metal droplet machine
Abstract
Magnetism and magnetic monopoles are among the most classical issues in physics. Conventional magnets are generally composed of rigid materials and may face challenges in extreme situations. Here, as an alternative to rigid magnets, we propose, for the first time, the generation of fluidic endogenous magnetism and construct a magnetic monopole through tuning with a liquid metal machine. Based on theoretical interpretation and conceptual experimental observations, we illustrate that when liquid metals, such as gallium alloy, in a solution rotate under electrical actuation, they form an endogenous magnetic field inside. This explains the phenomenon where two such discrete metal droplets can easily fuse together, indicating their reciprocal attraction via the N and S poles. Furthermore, we reveal that a self-fueled liquid metal motor also runs as an endogenous fluidic magnet owing to the electromagnetic homology. When aluminum is added to liquid gallium in solution, it forms a spin motor and dynamically variable charge distribution that produces endogenous magnetism inside. This explains the common phenomena where reflective collision and attractive fusion between running liquid metal motors occur, which are partially caused by the dynamic adjustment of their N and S polarities, respectively. On this basis, more experimental approaches capable of generating dynamic electrical fields also work for the same target. Finally, we propose that such a fluidic endogenous magnet could lead to a magnetic monopole and four technical routes to realize this are suggested. The first involves matching the interior flow of liquid metal machines. The second is the superposition between an external electric effect and the magnetic field. The third route involves composite construction between magnetic particles and a liquid metal spin motor. Finally, chemical methods, such as via galvanic cell reactions, are proposed. Overall, the present theory and identified experimental evidence illustrate the role of a liquid metal machine as a fluidic endogenous magnet and highlight promising methods for the realization of magnetic monopoles. A group of unconventional magnetoelectric devices and applications could therefore be possible in the near future.
Keywords
INTRODUCTION
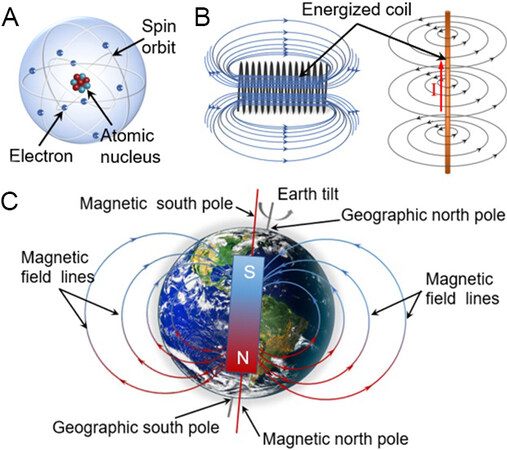
Magnetism and magnetic monopoles are two of the most fundamental and intriguing issues in physics and science in general. Although magnetic fields are invisible and intangible, they are unique phenomena that exist objectively and can be found at a huge range of scales from cells to stars. So far, researchers have conducted many in-depth studies on various existing known magnetic fields[1,2], including those in coils, the Earth, galaxies and so on, as shown in Figure 1A-C. Magnets exert forces and moments on each other through their respective magnetic fields. With the aid of the magnetic field as a medium, an object can transmit a magnetic force without contact. The study of magnetic fields is of great significance to scientific and technological progress in fields such as electronic cooling[3], microfluidic chips[4], orientation control of graphene[5], medical imaging and tumor treatment[6-8], visual probing of amino acids[9], magnetic proteins[10], magnetotactic bacteria[11,12] and so on.
Figure 1. Several typical types of magnetic fields. (A) Inside an atom. (B) An energized coil. (C) The Earth.
According to modern physics, the magnetic field produced by moving charges [Figure 1A] is fundamentally determined by moving electrons or protons. The atom is the smallest basic unit that makes up a substance and the magnetism of a substance is the collection of the magnetism of all the atoms it contains. Inside the atom, the electrons outside the nucleus rotate while moving around the nucleus. The above motion generates minute circular currents. According to Maxwell’s electromagnetic theory, electricity and magnetism are induced by each other and these minute circular currents excite a corresponding magnetic field. Therefore, the magnetic field generated by a current or point charge is the macroscopic manifestation of the magnetic field generated by a large number of moving electrons or protons.
Traditionally, from microscopic magnetic nanoparticles to macroscopic natural magnets, as well as artificially manufactured excitation coils [Figure 1B], permanent magnets are composed of rigid materials and their N and S poles are located at opposite ends. Generally, the shape and structure of such magnets cannot be changed on the eigenscale, which makes their applications somewhat limited. In order to improve the adaptability of magnets to different situations, researchers have invented magnetic fluids as functional materials, which are colloidal solutions formed by surface active agent-encapsulated nanomagnetic particles dispersed in base fluids[13] and show special magnetic and optical properties. Although their fluidity has been enhanced, the part that exhibits magnetism has not deviated from the essence of a conventionally rigid magnet. Recently, as a base fluid material for loading magnetic nanoparticles, liquid metals have been gradually developed as multi-functional materials due to their outstanding electrical and thermal conductivity and ductility. In particular, the chemical properties of room-temperature liquid eutectic alloys, such as GaIn and GaInSn, are relatively stable under normal conditions. Their low toxicity and good operability allow researchers to adjust the alloy ratio to achieve various characteristics to make them competent for tasks that rigid materials cannot do.
Previous studies on the magnetic properties of liquid metals have mostly involved the addition of iron particles[14] or chemically coating nickel on the surface of the droplet[15] and then using magnets to manipulate the composite material. The orientation of the magnet causes a change in the motion state of the droplet. Even when the position of the droplet is unknown, the magnet can attract it rapidly. However, this has not been the end of their development. Over the past decade, we have observed a series of very unconventional liquid metal machine behaviors that were either actuated by external fields or simply self-powered. It is based on this abundant experimental evidence that we conceive here that, on a microscopic level, when excited by an internal or external current during the rotational process, a spherical liquid metal droplet will form an endogenous magnetic field inside. This means that a fluidic spin magnetism is automatically generated. This rapidly rotating liquid metal droplet not only possesses the magnetic properties of rigid materials but also flows like water. These droplets represent a new type of magnetic matter that we term fluidic magnets.
Furthermore, we propose that fluidic magnets offer another important clue to answering the classical issue of magnetic monopoles, which remain one of the most long-lasting scientific mysteries in nature. Previously, when researchers have tried to tackle the fundamental problem of whether magnetic monopoles exist or not, they have attempted to find solutions in rigid magnets, which might not always be rational in reality. Magnetic poles exist in the form of magnetic dipoles, forming countless closed loops of magnetic field lines. This fixed form of magnetic field distribution limits the routes to verify the actual existence of magnetic monopoles. So far, magnetic monopoles only appear as quasi-particles in condensed matter, such as the flipping excitation of spin ice[16-18] and the similar structure produced by the vortex of super-cold rubidium atoms in a Bose-Einstein condensate (BEC)[19]. However, as transformable fluidic conductors, liquid metal machines could generate a dynamically changing endogenous magnetic field in their random spin motion. When an external electric or magnetic field is superimposed, compounded with magnetic particles or even just artificially modified through internal chemical reactions, much more diverse magnetic field configurations and behaviors will be generated and magnetic monopoles may be possible. This principle and mechanism are fundamentally different from conventional rigid magnetic materials with fixed poles. The present study is dedicated to profiling a new conceptual fluidic magnet and providing several potentially feasible technical routes towards finding and constructing magnetic monopoles or their composites.
EXPERIMENTAL
The rather profound basic properties of conductive fluidic metals endow them with many unconventional capabilities in realizing the currently proposed fluidic endogenous magnetism. Generally, at the macro level, the flexibility or rigidity of a material has an important impact on its application. In recent years, with the development of materials science, various unique effects of soft matter have been gradually discovered and utilized. In particular, room-temperature liquid metals possess many favorable properties[20-26], including large surface tension, ideal flexibility, high conductivity, low toxicity and so on. Furthermore, their excellent electric conductivity molds them into intrinsically conductive fluids. Table 1[27] lists some of the typical properties of gallium-based liquid metal and comparative liquids. Due to the different component ratios, the physical properties of such liquid metals appear somewhat different[22,23,25,26]. It should be noted that systematic measurements and currently available data for these materials remain rather limited. The deviation among different sources sometimes may be large, which increases the need for further research. However, no matter which kind of liquid metal is adopted, the conclusion in the present work is decided based on the most rational. The present strategy to generate fluidic endogenous magnetism has a generalized purpose. Basically, it should be noted that even other electrically conductive solutions, such as aqueous NaOH, NaCl and so on, may also display similar fluidic endogenous magnetic behavior as liquid metals. However, for brevity and considering the huge conductivity of liquid metals, such electronic fluids are likely to play a dominate role in developing various forms of fluidic magnetism and are therefore the focus of the current experimental and theoretical analysis.
Typical physical properties of Ga-based liquid metal and other liquids[27]
| Composition | Ga | Ga75.5In24.5 | Ga67In20.5Sn12.5 | Ga61In25Sn13Zn1 | Hg | Water |
| Melting point (°C) | 29.8 | 15.5 | 10.5 | 7.6 | -38.8 | 0.0 |
| Boiling point (°C) | 2204 | 2000 | > 1300 | > 900 | 883 | 100 |
| Density (kg/m3) | 6080 | 6280 | 6360 | 6500 | 13530 | 1000 |
| Electrical conductivity (S/m) | 3.7 × 106 | 3.4 × 106 | 3.1 × 106 | 2.8 × 106 | 1.0 × 106 | - |
| Thermal conductivity (W/m·K) | 29.40 | 26.00 | 16.50 | - | 8.34 | 0.60 |
| Kinematic viscosity (m2/s) | 3.24 × 10-7 | 2.70 × 10-7 | 2.98 × 10-7 | 7.11 × 10-8 | 13.50 × 10-7 | 1.00 × 10-6 |
| Surface tension (N/m) | 0.700 | 0.624 | 0.533 | 0.500 | 0.500 | 0.072 |
| Sound speed (m/s) | 2860 | 2740 | 2730 | 2700 | 1450 | 1497 |
| Water compatibility | Insoluble | Insoluble | Insoluble | Insoluble | Insoluble | - |
As gradually realized by recent studies, the excellent characteristics of liquid metals have seen their utilization in the fields of fluidics [Figure 2A], printed circuits [Figure 2B], flexible sensors, transformable machines [Figure 2C], self-driving motors [Figure 2D] and base carrier fluids for magnetic particles [Figure 2E]. The present research focuses on the electromagnetic effects of such fluidic conductive materials. In particular, the shape and motion of liquid metals have great variability and controllability, meaning that the magnetic fields generated will thus have rather rich application possibilities. On this basis, we propose a generalized matter state, which can be termed as electromagnefluid, indicating a material that simultaneously possesses electronic, magnetic and fluid properties.
Figure 2. Typical features of liquid metals that may serve to make endogenous magnetic fields. (A) Fluidic behavior. (B) Conductive electronic ink, reproduced with permission from Yang et al.[28]. (C) Morphologically transformable machine, reproduced with permission from Sheng et al.[29]. (D) Self-fueled motor, reproduced with permission from Zhang et al.[30]. (E) Loadable by magnetic particles, reproduced with permission from Wang et al.[31].
In principle, any experimental approaches to generate dynamic electronic charge variation on a liquid metal machine can possibly be used to realize fluidic endogenous magnetism. Five technical approaches are studied here. These include magnetism induced from a liquid metal energized coil, which is induced by alternating electricity, endogenous magnetism generated by an electrically tunable liquid metal machine inside an aqueous environment, an endogenous magnetic field generated from a self-driving liquid metal motor, which also works in solution, liquid metal spin superimposed on an external magnetic field and a magnetic field generated from a liquid metal under a chemical solution environment. The experimental evidence for fluidic endogenous magnetism is explained in the following sections.
RESULTS
Magnetism induced from liquid metal energized coil
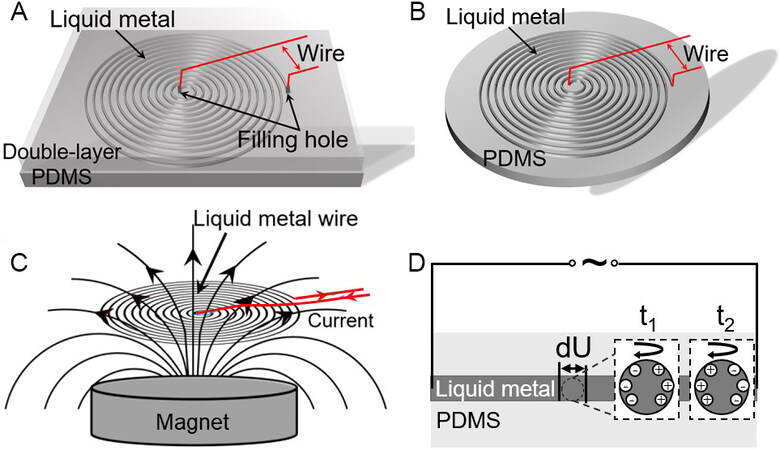
Liquid metals have good flexibility and conductivity and can replace traditional rigid coils, thereby making the moving parts of electromagnetic actuators more flexible and improving their ability to deal with complex situations. At present, there are two main methods to make liquid metal electromagnetic coils. The first is to apply optical mask technology to make microchannels on the polydimethylsiloxane (PDMS) substrate, followed by the injection of the liquid metal[32]. On this basis, the liquid metal is still in fluidic form [Figure 3A]. The other method is to use a mask with a specific shape to cover the PDMS substrate and uniformly print the liquid metal through a liquid metal spray gun [Figure 3B][33]. Compared to the first method, this direct printing method of liquid metal has a shorter production cycle and simpler operation. In this case, the liquid metal exists on the PDMS in a semi-solid form. The part in contact with air is oxidized but the liquid metal inside can still flow.
Figure 3. Schematic diagrams of liquid metal coil. (A) Method of injection. (B) Method of printing. (C) Magnetic field around the coil. (D) Partially enlarged view of the charge movement and rotation of the liquid metal in the coil.
In the magnetic driving device, the magnet is placed above or below the liquid metal electromagnetic coil [Figure 3C]. When applying an alternating current, the Lorentz force F is generated in the coil[33]:

where dU, as indicated in Figure 3D, is the potential difference between the two ends of the microsegment
For the first injection method, since the flow channel is in a sealed state and the operating temperature is higher than the freezing point of the liquid metal, the alloy in the flow channel is always liquid. Under the alternating electric field, the microsegment is subjected to an electromagnetic force and generates an endogenous magnetic field, which has an attractive or repulsive interaction with the placed magnet and other microsegments. However, this force is weak and only the device action dominated by the Lorentz force of the coil can be observed.
Endogenous magnetism generated by electrically tunable liquid metal machine
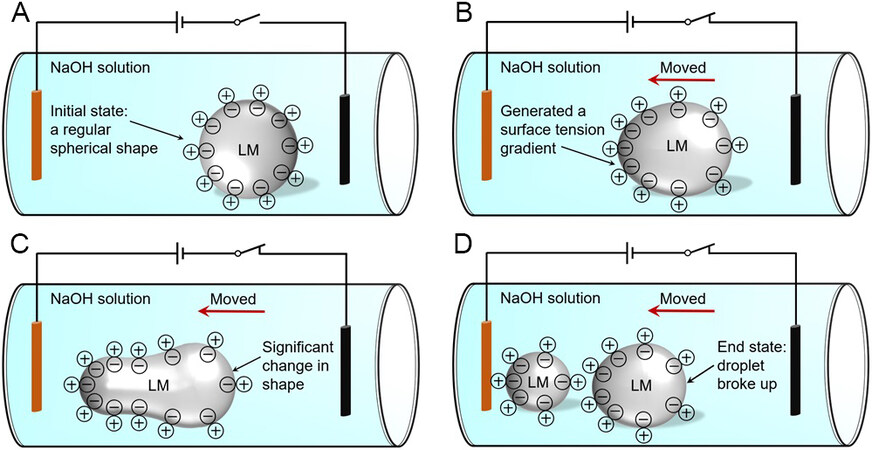
The application of an electric field to a liquid metal can induce its transformation, movement or rotation, and its motion state depends on the direction and strength of the applied electric field, the contact with the electrode and the surrounding solution environment[29]. To illustrate the basic principle of an electrically controlled liquid metal spin machine, we designed a cylindrical channel with a smooth surface and put a spherical liquid metal droplet in the electrolyte-filled solution [Figure 4A]. After applying an external field, the liquid metal immediately rotated and moved towards the anode. The original spherical droplet was stretched and showed obvious deformation. When the applied electric field was sufficiently large, the droplets were dragged instantaneously [Figure 4B and C] and even separated into two small droplets, as shown in Figure 4D.
Figure 4. Schematic of a liquid metal droplet moving to the anode and breaking up under the electric field. (A) Droplet as a regular sphere. (B) Droplet slightly deformed. (C) Droplet displaying an obvious head and tail. (D) Droplet break up.
Due to the differences in the physical properties between the liquid metal and the electrolyte solution, the electric field changes at the two-phase contact interface, thereby generating electrical stress. The GaIn liquid metal could react with the NaOH solution to generate [Ga(OH)4]-, which is specifically adsorbed to the Ga surface. In the Helmholtz layer, the surface of Ga was negatively charged due to the abundance of reactive electrons and the diffusion layer was positively charged, thereby forming an electric double layer (EDL).
In order to determine the distribution of charge on the surface of the liquid metal, we adopted a Zetasizer (Zetasizer Nano Series, Malvern, UK) to test the zeta potential. The principle is to combine dynamic light scattering with electrophoresis, which can convert the particle moving speed into the zeta potential of the particle surface. The results of the two tests under the same conditions are very similar. Most of the particles are 1000 nm in diameter and the polymer dispersity index indicates that the tested particles have a high degree of uniformity. According to the measurements [Table 2], the zeta potential of eutectic gallium-indium (EGaIn) in the NaOH solution is around -30 mV, which is consistent with the previous charge distribution theory regarding the EDL structure.
Zeta potential of EGaIn in alkaline electrolyte
| Parameter | T (°C) | Zeta potential (mV) | Mobility (m2/Vs × 10-8) | Particle size (nm) | PDI |
| Test 1 | 25 | -30.2 | 2.371 | 1012.0 | 0.285 |
| Test 2 | 25 | -29.7 | 2.327 | 999.8 | 0.291 |
Based on the Lippmann equation, we can establish a connection between the interfacial tension and potential difference as[30]:

where γ is the interfacial tension, c is the capacitance per unit area of the EDL, V is the potential difference of the EDL and γ0 is the maximum interfacial tension when V = 0.
According to the Young-Laplace equation, the pressure difference p between the solution and the liquid metal droplet can be expressed as p = γ·(2/r), so the pressure difference between the two hemispheres of the droplet is:

where r is the radius of the curvature of the droplet surface[34], γH refers to the hemisphere with higher interfacial tension and γL refers to the hemisphere with lower interfacial tension.
Therefore, the charge density changed the tension gradient, causing the two hemispheres of the droplet to have a pressure difference, so the droplet moves or even breaks up.
Using an electrode to drag a droplet and approach another in the solution, when the distance between them was small enough, they quickly fuse. This internal rotation caused by an external electric field was similar to the spontaneous rotation of the droplet after consuming aluminum, as explained in more detail in a later section.
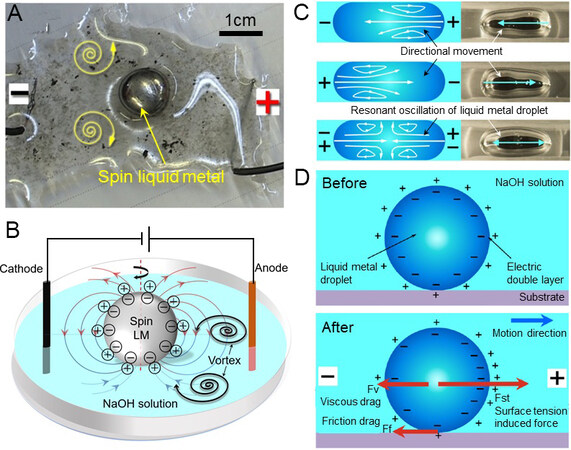
In the system composed of liquid metal and water, the influence of liquid metal on the surrounding water was obvious under the action of an external electric field. The system layout is shown in Figure 5A, with a spherical liquid metal droplet and a pair of electrodes placed in the solution. When the current was applied, the liquid metal sphere started to rotate, two eddies appeared in the surrounding solution and they kept rotating with the liquid metal sphere. Therefore, the external electric field could induce the liquid metal to rotate, thereby causing a real-time change of the charge distribution on the droplet. The moving charge enables the droplet to generate an endogenous magnetic field, as shown in Figure 5B.
Figure 5. Rotation and transformation of liquid metal in the solution under an external electric field. (A) Experimental case of rotating liquid metal droplet under direct current, reproduced with permission from Sheng et al.[29]. (B) Schematic for rotating liquid metal droplet under direct current. (C) Resonant oscillation phenomenon of liquid metal droplet under matching alternating field, reproduced with permission from Yang et al.[35]. (D) Electric field on the liquid metal-electrolyte interface before and after applying external electric field, reproduced with permission from Yang et al.[35].
Because the flow direction of the droplet surface was along the electric field gradient, when applying an alternating current, the direction of the electric field changed periodically and the flow state of the liquid metal also changes accordingly, as shown in Figure 5C. Before and after applying the external electric field, the electric field on the liquid metal-electrolyte interface changes [Figure 5D]. As the alternating frequency increased, the vortex current can become stronger and the magnetic field generated inside can be strengthened. It should be noted that such an endogenous magnetic field was a manifestation of electricity and magnetism on a microscopic level and its strength was much smaller than the magnetic field induced by the change in the external electric field.
Endogenous magnetic field generated from self-driving liquid metal motor
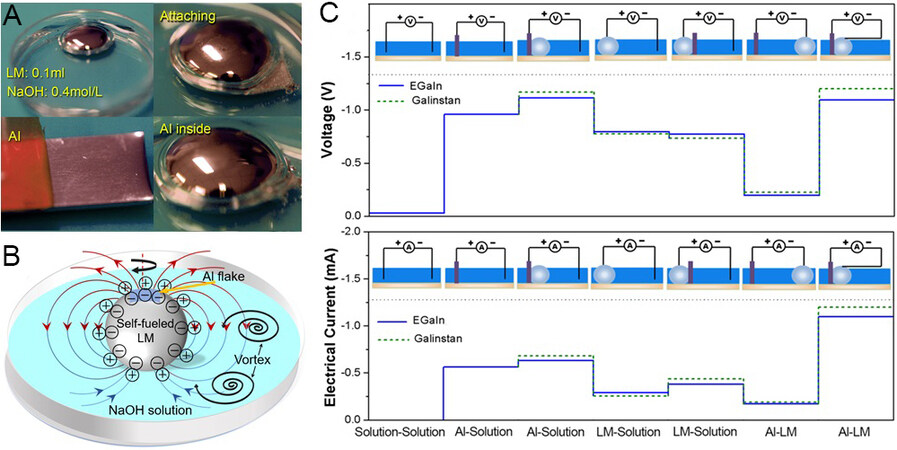
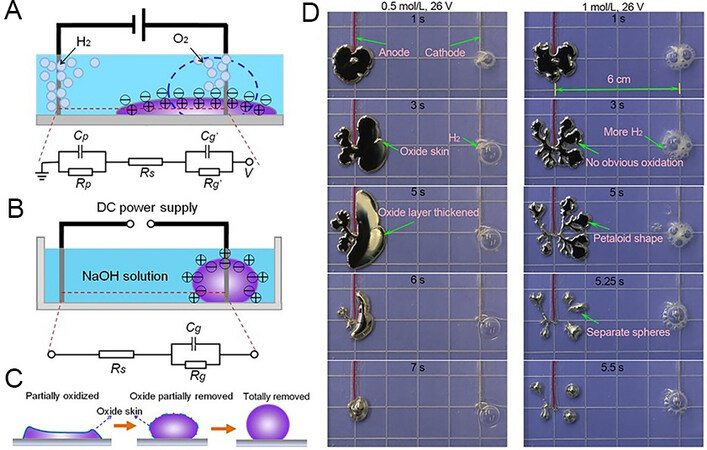
According to our former discovery, small liquid metal droplets possess an intriguing self-driving capability after being fueled with aluminum[36] and can automatically converge or diverge[37], which is a very unconventional feature that traditional rigid machines do not generally possess. According to the experiments, when placing a liquid metal droplet in the NaOH solution and adding some aluminum foil (as shown in Figure 6A), after a period of time, the aluminum foil is completely infiltrated and corroded by the liquid metal. The oxide layer on the aluminum surface then becomes destroyed, causing Al to activate, triggering a redox reaction, with the electrons from the aluminum interior preferentially deoxidizing the nearby oxidized gallium. Since the charge distribution of the EDL has already been changed, this results in a potential gradient and asymmetric surface tension on the surface of the droplet, which became the source of the driving force of the droplet motor[38].
Figure 6. Rotation and transformation of liquid metal in the solution after consuming aluminum. (A) Experimental case of rotating liquid metal droplet after consuming aluminum, reproduced with permission from Sheng et al.[39]. (B) Schematic for rotating liquid metal droplet after consuming aluminum and generated magnetic field. (C) Measured average voltage and electrical current on self-fueled liquid metal and electrolyte, reproduced with permission from Zhang et al.[30].
The liquid metal sphere moved randomly in the solution and was accompanied by its own rapid rotation, as shown in Figure 6B. Usually, its lifetime can last for more than 1 h without any other external energy depending on the fueled aluminum[30]. According to our former measurement, this self-fueled liquid metal motor generated electrical voltage and current between its surface and the surrounding electrolyte [Figure 6C]. It is this dynamically variable electrical field that leads to the generation of endogenous magnetism inside the liquid metal motor.
In addition, there was a galvanic reaction composed of liquid metal, aluminum foil and electrolyte solution, which accelerated the speed of the electrochemical reaction. After being corroded by the GaIn alloy, aluminum aggregated or dispersed on the surface. It was then uniformly distributed in the liquid metal in the form of small particles and hydrogen was generated by the electrochemical reaction [Equation (4)]. The average voltage and current between the liquid metal and the electrolyte could be measured by an AVOmeter[30], as shown in Figure 6C. The gas released from the interface also pushed the liquid metal forward to form a self-driving motor. When the size of the droplet was larger, the specific surface area was reduced and the electrochemical reaction sites were limited, resulting in less gas being generated and the driving force of the gas did not have an obvious effect on the large droplet. Therefore, the self-driving of liquid metal in a large volume mainly depended on the tension gradient.

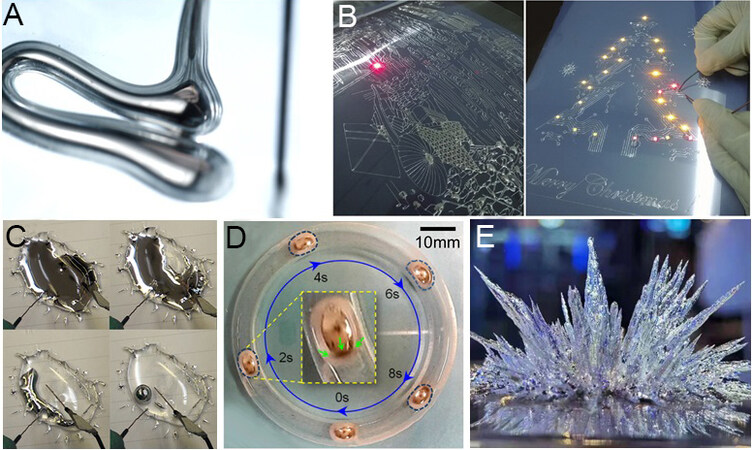
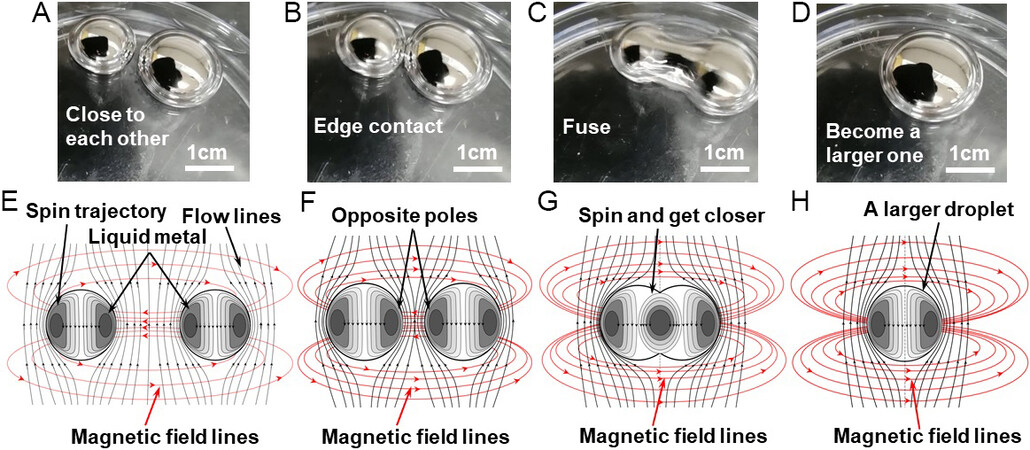
Next, we experimentally explored the fusion of rotating droplets [Figure 7]. In the solution, two liquid metal droplets rotated inside after swallowing aluminum, changing the flow line of the surrounding fluid[39]. When the distance was sufficiently small, they quickly fused.
Figure 7. Droplets fused, induced flow and magnetic field. (A-D) Experimental images of the fusion process of two droplets. (E-H) Spin trajectory of the liquid metal droplets and the surrounding flow lines.
In the electrolyte, the surface charge distribution of the two droplets was the same. Due to the electric repulsion, when two droplets run close to each other, there is mutual repulsion, rather than quick fusing. Therefore, we believe that this phenomenon was affected by the fluid dynamics and was also related to the internal magnetic field generated by the rotation of the droplet machine.
During the rotational process, through adaptive adjustment, magnetic fields were induced that attracted each other. The two droplets were brought closer and fused into one, as shown in Figure 7A-D. Over the process, endogenous magnetic fields were induced inside the liquid metal [Figure 7E-H]. The internal eddy current was similar to that excited by an external magnetic field and such an eddy current would generate a magnetic field in the sphere[40]. This mechanism allows discrete droplet motors to be quickly assembled, which has profound significance for self-assembly machines with internal triggering motion.
Liquid metal spin superimposed on an external magnetic field
Adding aluminum to the liquid metal can form tiny motors in the NaOH solution, but the movement is random and lacks a specific direction and speed[39]. If this kind of random movement can be controlled, the liquid metal self-driving motor can be used in more applications, such as transformable intelligent robots, precise drug delivery, detectors/sensors and so on. By placing a magnet under the Petri dish to introduce a magnetic field, the EGaIn liquid metal motor had a significant group effect at the boundary of the magnet. Over time, the motor group gathered near the boundary of the magnet and then rebounded after a short stay. Tan et al.[41] found and suggested that this peculiar phenomenon was related to the magnetic flux density of the bottom magnet and the magnetic field strength was zero at the boundary of the magnet. At first, these droplet motors were attracted by the magnet, which led to aggregation. The higher magnetic induction intensity on the side of the magnet prevented the motor from passing, while the peak of the magnetic field on the side away from the magnet was lower. The droplet motor selectively tended to the low peak position, thus limiting the motor’s range of motion.
Based on our former experimental observation[41], we tracked the motion path of a single droplet motor and carried out a more in-depth interpretation on the interaction mechanism between the liquid metal and the magnet. Here, we propose a conjecture that the spin liquid metal generated a magnetic field at a microscopic level. Since the motor was small and in a solution environment, the spin driving of the motor could more clearly show the characteristics related to the magnet. The magnetic field generated by the spin is non-directional and the droplet exhibited the same or opposite magnetic poles as the magnet at the boundary of the magnetic field, resulting in the effect of being repelled or attracted.
We studied the effect of the external magnetic field on the moving liquid metal droplet in the above phenomenon. From the present interpretation, the rotating liquid metal droplet generates a magnetic field and there are electrons flowing through it. The magnetic field intensity of a magnet around it is H and the magnetic induction intensity is B. The liquid metal sphere is then subjected to the Lorentz force of magnetic induction intensity on the charged sphere and the force of the magnetic field intensity on the sphere’s own magnetic field simultaneously. Firstly, we analyzed the Lorentz force on the sphere. Assuming that the moving speed of the liquid metal sphere is v and the overall charge is Q at a certain time, the liquid metal sphere can be regarded as a large charged particle. The force F1 can then be obtained from the Lorentz force formula in classical electromagnetics:

Using the equivalent magnetic charge theory, the stress of the liquid metal sphere in the magnetic field intensity can be obtained. Assuming that the magnetization of the liquid metal sphere is Mp and the magnetization in the solution is Ms, then the equivalent surface magnetic charge density on the surface of the liquid metal sphere κ is:

where μ0 is the vacuum permeability and n is the normal vector of the surface of the liquid metal sphere.
By integrating the surface S of the sphere, the magnetic force of the sphere under the magnetic field intensity is:
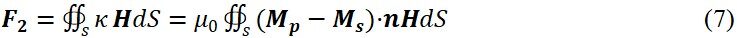
Therefore, the total force of the applied magnetic field on the liquid metal sphere in this system is:

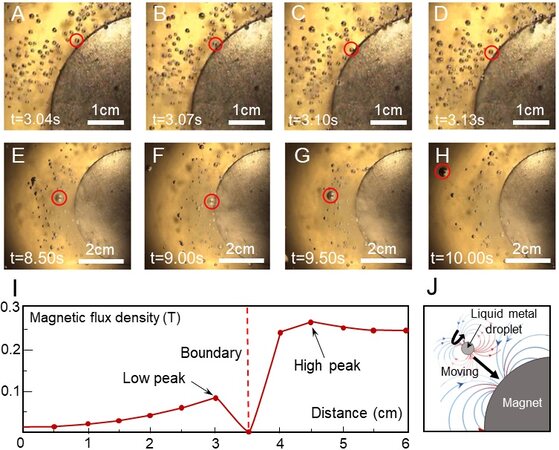
For a small-volume liquid metal motor, as shown in Figure 8A-D, the magnetic field strength was the smallest near the magnetic field boundary and the magnetic force on the droplet motor was weak. Therefore, the motor oscillated in a small range nearby. The force was converted into the momentum of the motor, making the momentum continuously accumulated. When the motor moved away from the magnetic field, the magnetic pole facing the magnet was the same as the magnet, which produced a repulsive force. When it reached a certain value, it could break away from the restraint of the magnetic field boundary, so it appeared to be bounced off by the magnet from a macroscopic perspective. Due to the increase of the magnetic field along the diameter of the magnet, the droplet far away from the magnet would be in a larger magnetic flux density space, the magnetic force would become more obvious and the momentum would further increase. Although the magnetic poles generated by the endogenous magnetic field might be attracted by the magnet at the next moment, the attractive force could not pull back the large momentum droplet away from the magnet, so the droplet eventually moved away from the magnet.
Figure 8. Motions of liquid metal motor under the action of magnetism. (A-D) Position of small liquid metal motor. (E-H) Position of large liquid metal motor, reproduced with permission from Tan et al.[41]. (I) Magnetic flux density along the diameter of the magnet. (J) Schematic diagram of magnetic interaction between liquid metal motor and magnet.
However, large-volume motors were not as sensitive to weak magnetic fields at the boundary of magnets as small-volume motors, as shown in Figure 8E-H. When the large-volume motor happened to approach the magnet with the same pole, it was hindered by the external magnetic field. In the process of approaching the center of the magnetic field, the motor’s potential energy continued to accumulate and the momentum gradually decreased. Under the continuous accumulation of reverse acceleration, the liquid metal motor began to move away from the magnet [Figure 8G] and the accumulated potential energy turn back to its own momentum. When the speed reached a certain level, it could break away from the restraint of the magnetic field boundary. We took a point 6 cm away from the center of the magnet as the starting point and measured the magnetic flux density on the connection between the two points, as shown in Figure 8I. Near the boundary of the magnet, the magnetic flux density changed greatly. Due to electromagnetic induction, an electric field and the corresponding magnetic field could be excited in the liquid metal.
Based on the above discussion, we suggest that when the motor had the same or opposite magnetism as the bottom magnet, it was repulsed or attracted [Figure 8J]. Simultaneously, the influence of the interfacial tension gradient on the motor movement cannot be ignored, resulting in the macroscopic effect of the motor group rotating, oscillating, gathering and bouncing off the boundary of the magnet, and this effect was affected by the volume of the motor.
Magnetic field generated from liquid metal under chemical environment
Liquid metal reacts with other metals to form a galvanic cell, which is also a way to cause spin. Liquid metal is easily oxidized in the air and forms an oxide layer on the surface, which is inconvenient to the observation and analysis of the surface and internal movement. Usually, we put the liquid metal in an acid or alkaline solution for operation to remove the surface oxide film, and on this basis, build a galvanic cell with other metals.
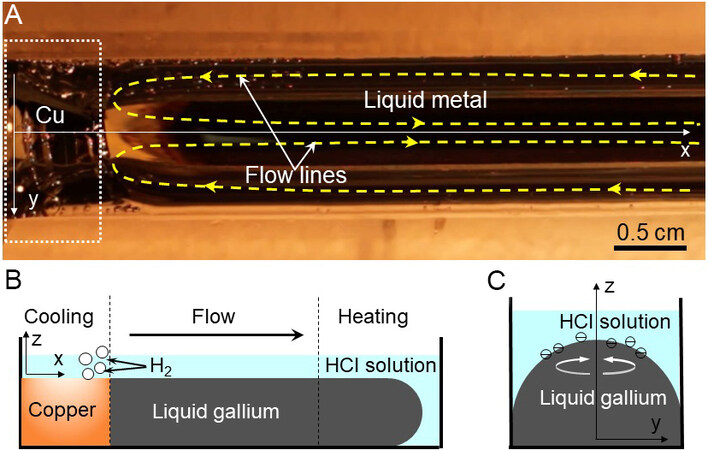
Previous studies revealed the Marangoni effect caused by a gallium-copper galvanic corrosion couple[42], with the tension gradient on the liquid interface moving the mass. Ga was oxidized to Ga3+ and the cathode had a corrosion potential between (Ga/Ga3+) and (H/H+), so H+ was reduced to H2 on the cathode [Equations (9) and (10)]. Therefore, the essence of the liquid metal Marangoni phenomenon was the galvanic corrosion.


Ga reacted with the HCl solution to produce gas at the liquid interface. By tracking the movement trajectory of the bubble, the flow state of the liquid metal could be obtained, as shown in Figure 9A. The liquid metal on the left was in contact with the copper and the flow lines of liquid gallium are marked in yellow. Here, the liquid metal participated in the reaction as a part of the galvanic cell and the internal rotation could make the charge flow through it [Figure 9B and C], which also had the conditions to excite the endogenous magnetic field.
Figure 9. Gallium-copper galvanic corrosion. (A) Superficial solution streamline, reproduced with permission from Tan et al.[42]. (B) The x-z plane view of galvanic corrosion system in the channel. (C) The y-z plan view of the liquid gallium and HCl solution in the channel.
In addition to the above-mentioned characteristics, liquid metal also has unique reversibility and it can control its structure via a synthetically chemical-electrical mechanism (SCHEME)[43]. As shown in Figure 10A, two platinum electrodes were inserted into the liquid metal and electrolyte. When direct current was applied, the gallium at the anode is oxidized to form Ga2O, Ga2O3 and so on, and the interfacial tension decreased. The originally spherical droplet appeared to spread out and the surface area increased, even reaching five times the original size. When the applied electric field was removed, the oxide layer on the surface chemically reacted with the NaOH solution, the interfacial tension of the droplet increased and it returned to the spherical state, as shown in Figure 10B-D. This reversible SCHEME was affected by many factors, such as current intensity, electrode spacing, liquid metal volume, electrolyte concentration and so on.
Figure 10. Reversible shape and charge redistribution mechanism of liquid metal, reproduced with permission from Zhang et al.[43]. (A) Experimental schematic diagram and equivalent circuit after applying DC power. (B) Experimental schematic diagram and equivalent circuit without external power supply. (C) Effect of surface oxide layer on droplet morphology. (D) Change process of droplet shape when the external power supply was removed after 5 s.
In this system that combines chemical dissolution and electrochemical oxidation, the liquid metal serves as both a conductor and a reactant. In the process of continuous expansion and contraction, the change in interfacial tension and the redistribution of charge could be achieved by controlling the external electric field. Over the process, the internal oscillations were synergistic with the movement of charges and the charges of such motions were also related to the dynamic magnetic field. Therefore, the internal chemical mechanism of liquid metal also had the possibility of generating an endogenous magnetic field. With this effect, one can possibly make up a programmable fluidic magnet in the near future.
THEORETICAL INTERPRETATION
Generation of endogenous magnetic field from liquid metal machines
When applying an external electric field or reacting with other metals to form a galvanic cell, the liquid metal acts as a conductor, current passes through its surface, the droplet forms a vortex inside simultaneously and it can be regarded as a charged spin conductor sphere. In fact, finding the magnetic field of a rotating conducting sphere under stationary conditions has never been a simple problem[44]. Based on some basic principles in classical electromagnetics, we conducted a theoretical analysis of this peculiar phenomenon and attempt to provide a more in-depth explanation. For the physical properties of the liquid metal spherical droplet, its density ρ, electrical conductivity σ and magnetic permeability μ0 are all constants. According to Maxwell’s electromagnetic equation, the space around a spherical droplet of liquid metal can be obtained as:




where its physical property equations are:



where H is the magnetic field strength (A·m-1), E is the electric field strength (V·m-1), B is the magnetic induction (T), J is the current density (A·m-2), D is the electric displacement (C·m-1) and ε is the dielectric constant.
Firstly, we analyzed the liquid metal droplet in the rotating state after consuming aluminum foil, as shown in Figure 11A and B. The liquid metal droplet, aluminum foil and electrolyte solution together constituted a galvanic cell, with aluminum foil as the cathode and liquid metal as the anode. For the rotating liquid metal droplet, its internal current was composed of two parts, the first part was the galvanic current I1 produced by the electrochemical reaction of the galvanic cell and the second part was the rotating current I2 produced by the charge moving in the rotating process. The current density of the liquid metal droplet was also composed of these two parts, J1and J2 respectively, and the synthetic magnetic field of the liquid metal droplet was generated under these two different currents.
Figure 11. Schematic diagram of the movement mechanism and equivalent circuit of surface current in a NaOH solution. (A) and (B) Liquid metal sphere consuming aluminum. (C) and (D) Under an external electric field.
We defined the angular velocity of the liquid metal droplet as ω. According to the measurement of the zeta potential, the liquid metal droplet is the carrier of charge. During the process of rotation, the charges move with the internal flow field and the charged surface, thereby determining the direction of the electron current. We supposed that when there was current flowing inside and the direction of the current was parallel to the rotation of the liquid metal droplet in dynamic equilibrium. The radius of the sphere of the liquid metal droplet is “a”, the center of the sphere is the origin, the axis of rotation is the polar axis to establish a spherical coordinate system and r is the distance from any point to the center of the sphere. Assuming that Q1 is the total charge passing through the maximum cross section (radius = a) of the liquid metal droplet within time t, the current passing through the maximum cross section can be equivalent to:

During time t, the current density flowing on any circular cross section perpendicular to the current direction on the sphere is:


where s1 is the area of the circular cross section, 0< r ≤ a and n1is the normal vector of surface s1.
For the second part, when the liquid metal droplet rotates, the charge on it moves accordingly. If a large amount of charge could maintain directional motion for a period of time, the current I2 would be formed. Assuming that in the process of constant rotation, the charge amount of the liquid metal droplet is Q2, then the volume charge density is:

The corresponding current density is:
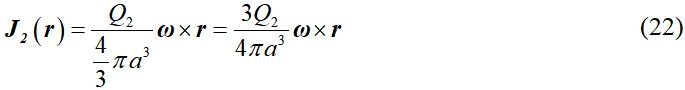
Under steady conditions, adopting the vector potential generated by current is a solution in the classical theory of electromagnetics. The vector potential of a point A (r1, θ, φ) outside the liquid metal droplet can be obtained as[45]:
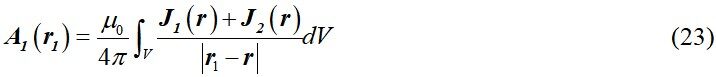
where |r1-r| is the distance between point r1 (r1, θ1, φ1) and point r (r, θ, φ).
According to the basic equation under steady electric fields, the galvanic current and the rotating current flowing through the liquid metal droplets can be obtained together at any point A outside the body. The resulting expression of the total magnetic induction is:

Next, we analyzed the liquid metal sphere rotating under an external electric field, as shown in Figure 11C and D, similar to the previous analysis. The only difference is that the liquid metal sphere droplet does not have the current generated by the galvanic reaction but has an external conduction current under the external electric field. When an electric field is applied, the liquid metal droplet in the electrolyte solution not only conducts current but also forms a rotating current. In this case, it is also assumed that I3 is the conduction current flowing through the largest cross-section (r = a) of the sphere and then the current density flows on the circular cross section perpendicular to the current direction is:

where n2 is the normal vector of surface s2.
Similarly, it is assumed that liquid metal droplets will also generate a rotating current I4. During the constant rotating process, they always have a charge of Q4, so the charge density is:

and the current density is:
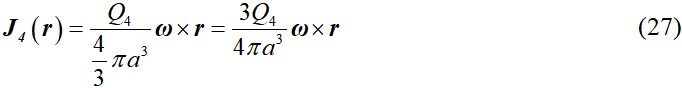
Similar to the above analysis, the vector potential of any point B (r2, θ, φ) outside the body of the liquid metal droplet can be obtained as:
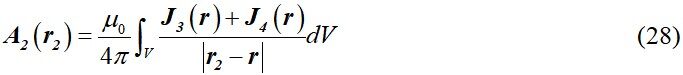
where |r2-r| is the distance between point r2 (r2, θ2, φ2) and point r (r, θ, φ).
The liquid metal droplet under an external electric field is then integrated by the conduction current and the rotating current, and the total magnetic induction intensity generated at any point B outside the body is expressed as:

Through the analysis of the above two motion phenomena of the liquid metal sphere droplet, it can be seen that when the liquid metal droplet rotates in the solution, there is current passing through it and the sphere itself will also generate a rotating circular current. The superimposition of these two currents generates a magnetic field. In fact, the strength of the magnetic field is also restricted by the rotation speed and droplet’s volume and other factors, which have brought difficulties to theoretical calculations. However, through numerical simulation, the external, interfacial and internal flows of a droplet can be revealed. Simultaneously, due to the instability of the rotation of the liquid metal droplet on the plane, its motion state will suddenly change within a period of time, so the measured internal current and voltage are only average values. Therefore, the direction of the current and magnetic field in our basic model refer to the instantaneous state. This continuously changing state offers the magnetic field more possibilities. Furthermore, if one-to-one manipulation is performed on the smaller vortex inside, the electron current will have more maneuverability and the complex magnetic field that is excited should be analyzed accordingly, which is also a direction worthy of exploration in the near future.
The spin liquid metal, which is still in the form of a full fluid, is essentially different from the magnetic fluids widely reported previously. It is overall a weak magnetic substance. In this study, we tried to measure the magnetism with an mT-level magnetometer but no obvious results were obtained. Finer measurements of the magnetic field strength, such as μT, nT and even at the pT level, are possible directions in the future. However, it is noteworthy that rapidly increasing the rotation speed can speed up the movement of charges, as can changing the electric field rapidly. These potential methods may make it possible to realize a transient and perhaps stronger liquid magnetic field. They can also be used to adjust the rotation speed, volume and current in the rotation process and can be applied to various research applications that require flexible magnetic fluids by virtue of the characteristics of full fluids.
Technical routes to realize a magnetic monopole from liquid metal machines
Most liquid metal magnetoelectric devices and magnetic drive structures reported previously use an external electric field to change the overall magnetic field of the structure, thereby causing the device to act. For example, a spiral GaIn alloy was printed on PDMS to obtain a flexible electromagnetic driver[33]. When an alternating current was applied to the coil, the coil generated a magnetic field, which was attracted and repelled by the magnets on both sides according to the alternating frequency of the current and could simulate jellyfish swimming, fish tail swinging and other actions. There were also studies using the electromagnetic interaction between a magnet and a Galinstan liquid metal coil to generate sound waves and make a retractable dynamic acoustic device[46].
Traditional magnetic materials are almost entirely confined to solids. During the magnetization process, the magnetic domains of each tiny magnetized area are already oriented. Simply cutting magnets or putting a large number of small magnets together will not lead to a monopole because these are operations performed on magnetized materials. In fact, it is difficult to find a matching substance in traditional magnetic materials when searching for magnetic monopoles and it is even more difficult to find a case through experimental observation. Some researchers have obtained singular magnetic point defects at the quantum level. The magnetic whirl known as a skyrmion, which has a one-to-one association with a quantized magnetic flux and is created or destroyed at a certain point, can be regarded as a magnetic monopole and antimonopole[47].
However, a liquid metal can generate or offset endogenous magnetic fields in non-magnetic materials through its own rotation or spatially fluidic field tuning. While the internal eddy current generates a magnetic field, it can also excite a second eddy current[40], which would induce the second magnetic field and so on. The internal vortex in the spin liquid metal has a corresponding relationship with the magnetic field. Through the design of a multi-structure, multi-material and multi-phase, a singular point may appear under their interaction at a moment, where the magnetic field appears as only “in” or “out”, but the system is in an unstable state at this time. In this dynamic process, the system continuously adjusts itself to reach a steady state and return to the magnetic dipole situation. Just as the topological defect is defined as a magnetic monopole, combining an internal vortex with electromagnetics, whether there will be a singular point inside the liquid metal under the coupling of multiple fields is a question worthy of further exploration.
Considering the aforementioned five basic methods of exciting a magnetic field with a liquid metal, we propose the following potential technical strategies of artificially synthesizing a liquid metal sphere towards realizing a possible magnetic monopolar state.
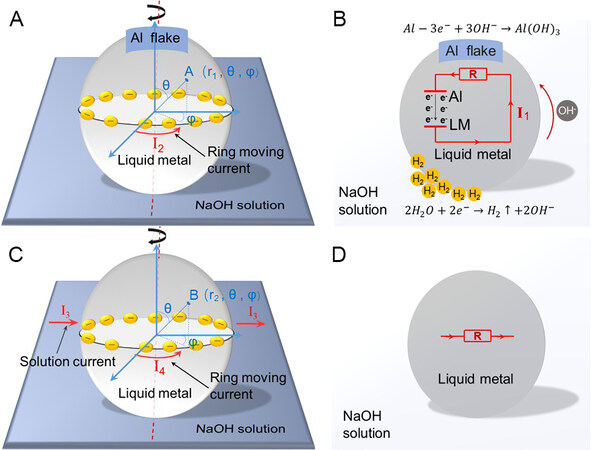
Route 1: matching the interior flow field of liquid metal droplet machines
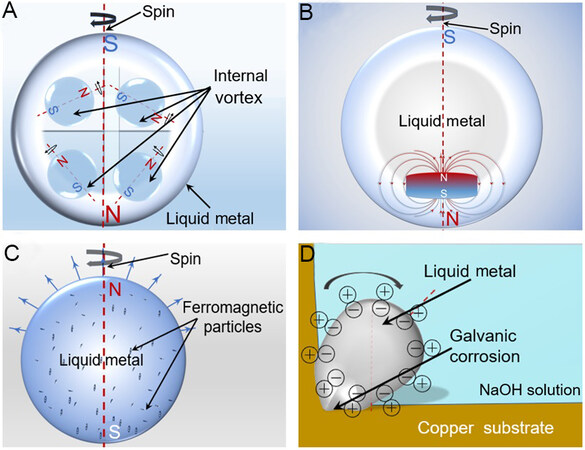
As shown in Figure 12A, while the liquid metal sphere rotates itself after consuming the aluminum foil, there may be vortexes inside which move opposite to the outer fluid. This uniquely nested structure makes it possible to artificially synthesize magnetic monopoles. When the outer sphere rotates around the axis, the inner four small spheres perform their respective circular motions in opposite directions. Then, through microscale manipulation, such as regulating the position and speed of the rotation, the N or S pole in the outer area and the magnetic poles generated by the four small vortexes in the interior can possibly mutually offset, so that the entire liquid metal sphere exhibits only a single magnetic pole.
Route 2: superposition between external electric effect and magnetic field
Secondly, an external field superposition method can be adopted. As shown in Figure 12B, a tiny magnet is inserted into the end of the liquid metal sphere. When the liquid metal sphere is spinning, the magnet is fixed, so that the magnetic field of the magnet and the magnetic field generated by the spinning liquid metal sphere are superimposed. When the two cancel out at a certain moment, the remaining magnetic field is located at the end far away from the magnet. At this time, the liquid metal sphere exhibits such magnetism that is not cancelled.
Route 3: composite construction between magnetic particles and liquid metal motor
Adding appropriate magnetic nanoparticles into the liquid metal sphere is also a possible method, as shown in Figure 12C. Since the ferromagnetic particles are very tiny, when they are uniformly mixed with the liquid metal spheres, the spinning liquid metal spheres also generate many tiny magnetic fields. The endogenous magnetic field can also interact with the ferromagnetic particles loaded. Proper control of the number, shape and position of magnetic nanoparticles may also make up the synthetic magnetic field of the liquid metal sphere to exhibit possible unique characteristics.
Route 4: chemical routes (such as via galvanic cell reactions) between liquid metal motor and substrate or foreign substances
Finally, chemical reactions remain a possible option, as shown in Figure 12D. As mentioned above, when the copper contacts liquid metal to form an electrode pair, a galvanic cell that can undergo electrochemical reactions is formed in the solution. When the current flows through the liquid metal, the droplet spins under the surface tension gradient. In such an environment where two different metals are in contact with each other, the simultaneous manipulation of another metal substrate (like copper) and a spinning liquid metal sphere is allowed, so that the sphere produces a synthetic magnetic field with potential monopole characteristics.
Overall, we have identified several potential techniques that may offer new possibilities for exploring magnetic monopoles or their composite structures. In the above diverse methods of constructing the magnetic monopole, the control of the spin vortex inside the liquid metal is a certain challenge due to the changeable rotation state. So far, due to limitations with the current testing methods, we mainly outlined the major conjecture in the area. Through artificial control, it is possible to synthesize a magnetic substance that acts as a source or sink of magnetic field lines by using the spin characteristics of the liquid metal machine, which is expected to provide supporting evidence for the actual existence of magnetic monopoles in the near future.
DISCUSSION
Classical magnetic monopole theory
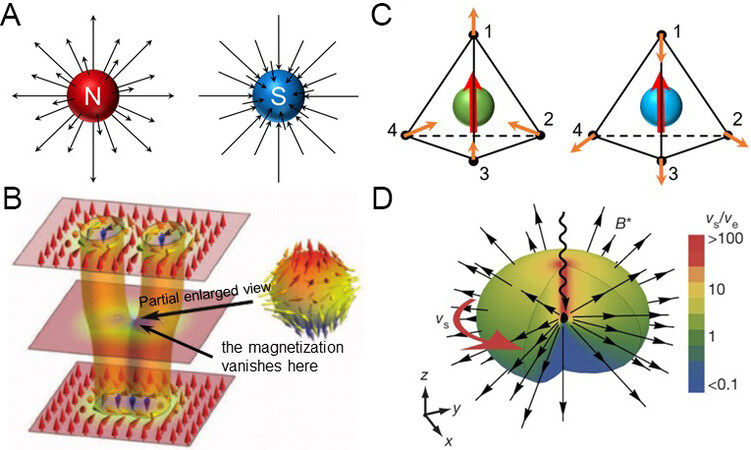
Under active vacuum conditions, Maxwell’s equations do not satisfy the invariance of electromagnetic duality. Electrons are regarded as the source and sink of electric field lines, implying that particles with basic magnetic charges are related to the emission of magnetic field lines. Therefore, Dirac[48] proposed the magnetic monopole theory in 1931 to resolve this problem. A magnetic monopole is a magnetic substance with only a single magnetic N or S pole in theoretical physics and its magnetic line of induction is similar to the electric field lines of a point charge, as shown in Figure 13A. Dirac[48] used a mathematical formula to assess its existence by analyzing the phase uncertainty of the wavefunction of a quantum system. It is noteworthy that if the magnetic monopole really exists, the electric and magnetic charges must be quantized in quantum mechanics. In modern physics, charge quantization has become an important theory and it has also inspired tremendous research in the search for magnetic monopoles.
Figure 13. Hypothesis and simulation of magnetic monopoles. (A) Conceptual diagram of magnetic monopoles. (B) Sketch of a magnetic configuration describing the merging of two skyrmions, reproduced with permission from Milde et al.[47]. (C) Schematic diagram of spin ice excited state. (D) Magnetic monopole model composed of a cold atom condensed state, reproduced with permission from
In order to find magnetic monopoles, researchers have conducted tests and experiments for decades. A well-known theory related to magnetic monopoles is the grand unified theory (GUT), in which strong interaction forces, weak interaction forces and electromagnetic forces could be unified into a normative interaction. Unlike elementary particles, a magnetic monopole is a regional energy known as a solitary wave and its size and mass could be estimated through the unified field theory. The quality of a magnetic monopole was ~1016 GeV[49,50]. Simultaneously, the internal space freedom of the gauge theory made the magnetic monopole have a certain topological structure and provided stability. Although the GUT was dedicated to unifying the interaction forces between microscopic particles, it had not been finally verified, nor can it solve problems such as the “excess” of magnetic monopoles[51]. In addition, string theory, M-theory (where M refers to magic, mystery, membrane and matrix) and so on have also conjectured the existence of magnetic monopoles.
Extension of magnetic monopole concepts
Beyond the classical theory, some physicists have turned to mathematical approaches to find possible clues towards magnetic monopoles. For example, Yang and Wu[52] introduced the overlapping area of the sphere to construct a dual coordinate system to eliminate singular chords. They proved that any curl of the two vector potentials could reasonably give the magnetic field of a monopole and gave a magnetic monopole solution in the overall description of the gauge field, namely, the Wu-Yang magnetic monopole. Abrikosov[53] proposed that the quantum state on the sphere of graphene was related to monopole harmonics. Under certain operators, keeping the magnetic monopole at the center of the sphere unchanged, rotating the sphere produces a part related to spin and this part was caused by a magnetic monopole.
On the basis of rich theories, some researchers have tried to explore the existence of magnetic monopoles through experiments, for example, by manipulating the external field and magnetic whirls[47], as shown in Figure 13B, or artificially constructing a magnetic monopole at a nano-magnetic needle[54]. Fang et al.[55] found that there was an anomalous Hall effect in ferromagnetic crystals and only the hypothesis of the existence of magnetic monopoles could explain this phenomenon. This result might serve as indirect evidence for the existence of magnetic monopoles in the momentum space of the crystal.
Because spin ice exhibits unique magnetic field characteristics, some recent studies have found analogues of magnetic monopoles in strange spin ice[16-18]. This is due to the dipolar magnetic excitation caused by the spin flipping that produces free defects distributed in the crystal lattice [Figure 13C], thus exhibiting the properties of a magnetic monopole[56], which has magnetic charges and electric dipoles[57], but it could not be separated from the material[18]. Dusad et al.[58] used a superconducting quantum interference device to detect the quantization jump of the magnetic flux of a Dy2Ti2O7 crystal and found that the magnetic noise generated by the magnetic monopole could be heard by humans after amplification. This was the most intuitive observation of magnetic monopoles in spin ice so far.
In condensed matter physics, theoretically, the spin structure of a BEC can be manipulated with point-like topological defects through an external magnetic field[59]. On this basis, Ray et al.[60] used cold atoms to generate Raman transitions from lasers of different frequencies under a magnetic field gradient to simulate the effect of the magnetic field. Since the magnetic spin arrangement of rubidium atoms was controllable, the magnetic spins were arranged in the form of large vortices and the middle part would have the effect of synthesizing magnetic monopoles. At this time, the spin direction of the atom could point to a certain point in space simultaneously, which also proved the basic quantum characteristics of the magnetic monopole, as shown in Figure 13D.
Experimental challenges and a new dawn for fluidic magnets
Although abundant evidence for the existence of analogues of magnetic monopoles has been found, the direct observation of Dirac monopoles in the medium of a quantum field has not yet achieved a breakthrough. For decades, with the support of the GUT, string theory, M-theory and other theories, researchers have even searched for relevant magnetic monopole trajectories in particle accelerators and lunar geotechnical sampling. Although researchers have not yet observed its actual existence by experimental means, liquid metal combines the properties of electrical conductors, magnets and fluids, which endorse its rather profound possibilities. When an electric or magnetic field is applied, or a galvanic cell is formed with other metals, the interior flow field will maintain a moving state, which is closely related to the movement of the electric charge and the excitation of the endogenous magnetic field. On this basis, the rich operability of liquid metal machines offers several possible experimental approaches for the discovery of magnetic monopoles.
The magnetic field described by Maxwell's electromagnetic equations is a passive field, where each closed magnetic line of induction does not have a starting or end point. If the magnetic monopole exists, the magnetic field will become an active field. Maxwell’s equations need to undergo appropriate coordinate transformation and conditional restrictions, which do not violate its correctness. The revised equations are as follows:


Compared with Maxwell’s equations, which originally did not consider the existence of magnetic monopoles, the two differential equations related to the magnetic field have changed. Since the magnetic monopole may also excite the electric field, the magnetic density vector Jm is introduced into Equation (12) to obtain Equation (30). Simultaneously, the magnetic monopole can excite the magnetic field by itself and the divergence of the magnetic field is no longer zero [Equation (31)]. The equations will show a more symmetrical electromagnetic field excitation form. Under the new category of liquid metal magnetic monopoles, many theoretical and experimental works are worthy of pursuing in the near future.
Endogenous magnets from rigid, soft to fluidic matter
From the initial discovery of natural magnetic fields, the manufacture of artificial magnets, to the conclusion of electromagnetic related theories, they took people a lot of time to explore. Based on the above systematic interpretation, we outline Figure 14 as follows, which comparatively illustrates the evolution diagram of various forms of magnets that have been manufactured so far, i.e., from rigid matter to soft materials until fluidic magnetism.
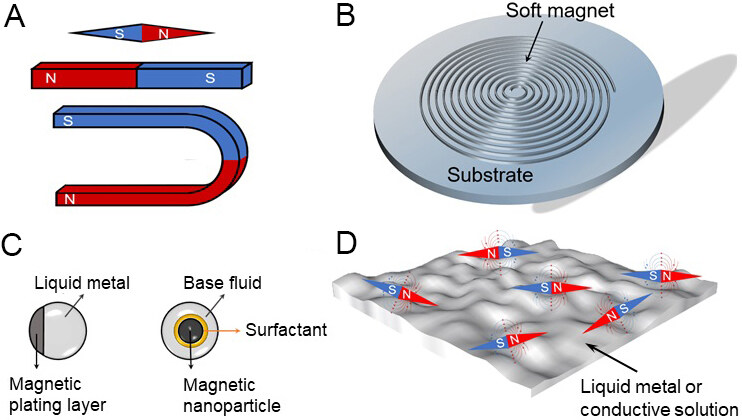
Figure 14. Different forms of magnets. (A) Rigid magnet. (B) Soft magnet. (C) Semiliquid magnet. (D) Liquid magnet.
Figure 14A depicts magnets of various shapes that are widely known and commonly used in daily life. Many important electromagnetic field theories are based only on these. Figure 14B refers to a soft magnetic substance, which can be attached to a specific substrate. This magnetic material has been applied in various electronic devices, such as sensors and flexible circuits. Figure 14C presents a composite of magnetic nanoparticles and fluid proposed in recent years. This fluid has no magnetic attraction in the static state and only exhibits magnetism when an external magnetic field is applied. It has a wide range of applications in the fields of medical equipment and magnetic fluid beneficiation but is still not an ideal all-magnetic fluid. Furthermore, the rotating liquid metal machine or motor, as proposed in this work, belongs to an entirely new kind of magnetic fluid or electromagnefluid, as shown in Figure 14D. In this category, there is no need to add additional magnetic particles, which is a complete magnetic fluid in the truest sense. The discovery of a full magnetic fluid based on a room-temperature liquid metal will bring new opportunities and directions for research in diverse fields, which has profound significance for the understanding of magnets and their full use.
In nature, the N and S poles always exist simultaneously. Each tiny magnet possesses N and S poles, which makes it difficult to achieve the existence of one pole alone. Compared with traditional rigid magnets, the advantage of liquid metal lies in its fluidity, which makes it easier to adjust to different shapes and the restriction on particle movement is reduced. When the surface charges move, the fluid inside keeps rotating, making the endogenous magnetic field in a state of constant change. If the single charge on the surface or the vortex inside of the liquid metal can be manipulated or the direction of electromagnetic particles reversed, it is possible to construct a liquid metal magnetic monopole.
Furthermore, once the direct experimental observation of the magnetic monopole has been achieved, the charge quantification can be better explained. Electrons are particles with no internal structure. They can be reshaped to carry orbital angular momentum. By coupling the center of mass of the wavefunction with the interior, the total angular momentum information will be obtained from the vortex beam and it can then be manipulated artificially[61]. Similarly, if the magnetic moment of the liquid metal micromotor can be measured to obtain momentum information, it may be manipulated and improved microscopically, and it will even be possible to develop technology based on moving magnetic charges to break through the limitations of current charge engineering and create magnetic materials that exhibit ever richer behavior.
CONCLUSIONS
Liquid metal can interact with sound, light, heat, electricity and magnetism. The present study disclosed for the first time that as fluidic conductors with charges, liquid metal machines open a generalized method for the generation of transformable endogenous magnets through the tuning of their spin states and interior rotational or moving configurations. This mechanism is rather difficult to implement through rigid materials otherwise. It may change our basic understanding of classical magnetism. A most noteworthy content in this finding still lies in that such a fluidic magnet suggested a new promising method to realize a magnetic monopole in reality. The fundamental routes can be based on either self-fueled liquid metal motor or the electrically controlled spin motion of liquid metal machine inside the electrolyte. Meanwhile, such liquid metal endogenous magnetism is fundamentally different from the conventional magnetic fluids, which was in fact caused by the magnetic particles rather than the fluid itself. This raised important fundamental and practical issues waiting to be addressed. It also opens perspectives for making new conceptual liquid machines, which may find some emerging uses in future basic physics, information technology, smart devices, advanced functional materials and intelligent system. Overall, the reasonable conjecture as made on the classical question of whether magnetic monopoles exist or not would shed light to innovate future science and engineering.
DECLARATIONS
Authors’ contributionsWrote and interpreted the manuscript: Zhou YX, Zu JS
Conceived and supervised the work, wrote and interpreted the manuscript: Liu J
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was partially supported by the National Natural Science Foundation of China (No. 91748206; No. 51890893).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationWritten informed consents for publication were obtained.
Copyright© The Author(s) 2021.
REFERENCES
1. Schneider FRN, Ohlmann ST, Podsiadlowski P, et al. Stellar mergers as the origin of magnetic massive stars. Nature 2019;574:211-4.
2. Hilger A, Manke I, Kardjilov N, Osenberg M, Markötter H, Banhart J. Tensorial neutron tomography of three-dimensional magnetic vector fields in bulk materials. Nat Commun 2018;9:4023.
3. Ma K, Liu J. Liquid metal cooling in thermal management of computer chips. Front Energy Power Eng China 2007;1:384-402.
4. Jiménez-Martínez R, Kennedy DJ, Rosenbluh M, et al. Optical hyperpolarization and NMR detection of 129Xe on a microfluidic chip. Nat Commun 2014;5:3908.
5. Lin F, Zhu Z, Zhou X, et al. Orientation control of graphene flakes by magnetic field: broad device applications of macroscopically aligned graphene. Adv Mater 2017;29:1604453.
6. Chi Z, Yi Y, Wang Y, et al. Adaptive cylindrical wireless metasurfaces in clinical magnetic resonance imaging. Adv Mater 2021;33:e2102469.
7. Espinosa A, Reguera J, Curcio A, et al. Janus magnetic-plasmonic nanoparticles for magnetically guided and thermally activated cancer therapy. Small 2020;16:e1904960.
8. Liu JF, Lan Z, Ferrari C, et al. Use of oppositely polarized external magnets to improve the accumulation and penetration of magnetic nanocarriers into solid tumors. ACS Nano 2020;14:142-52.
9. Xu Y, Yang G, Xia H, Zou G, Zhang Q, Gao J. Enantioselective synthesis of helical polydiacetylene by application of linearly polarized light and magnetic field. Nat Commun 2014;5:5050.
11. Blondeau M, Guyodo Y, Guyot F, et al. Magnetic-field induced rotation of magnetosome chains in silicified magnetotactic bacteria. Sci Rep 2018;8:7699.
12. Li Q, Chen H, Feng X, et al. Nanoparticle-regulated semiartificial magnetotactic bacteria with tunable magnetic moment and magnetic sensitivity. Small 2019;15:e1900427.
13. Shafi KVPM, Gedanken A, Prozorov R. Surfactant-assisted self-organization of cobalt nanoparticles in a magnetic fluid. Adv Mater 1998;10:590-3.
14. Guo R, Sun X, Yuan B, Wang H, Liu J. Magnetic liquid metal (Fe-EGaIn) based multifunctional electronics for remote self-healing materials, degradable electronics, and thermal transfer printing. Adv Sci (Weinh) 2019;6:1901478.
15. Zhang J, Guo R, Liu J. Self-propelled liquid metal motors steered by a magnetic or electrical field for drug delivery. J Mater Chem B 2016;4:5349-57.
16. Morris DJ, Tennant DA, Grigera SA, et al. Dirac strings and magnetic monopoles in the spin ice Dy2Ti2O7. Science 2009;326:411-4.
17. Bramwell ST, Giblin SR, Calder S, Aldus R, Prabhakaran D, Fennell T. Measurement of the charge and current of magnetic monopoles in spin ice. Nature 2009;461:956-9.
19. Gibney E. Quantum cloud simulates magnetic monopole. Nature 2014; doi: 10.1038/nature.2014.14612.
20. Wang MF, Jin MJ, Jin XJ, Zuo SG. Modeling of movement of liquid metal droplets driven by an electric field. Phys Chem Chem Phys 2017;19:18505-13.
21. Handschuh-Wang S, Chen Y, Zhu L, Gan T, Zhou X. Electric actuation of liquid metal droplets in acidified aqueous electrolyte. Langmuir 2019;35:372-81.
22. Handschuh-Wang S, Gan T, Wang T, Stadler FJ, Zhou X. Surface tension of the oxide skin of gallium-based liquid metals. Langmuir 2021;37:9017-25.
23. Tang S, Tabor C, Kalantar-zadeh K, Dickey MD. Gallium liquid metal: the Devil's elixir. Annu Rev Mater Res 2021;51:381-408.
24. Fu J, Liu T, Cui Y, Liu J. Interfacial engineering of room temperature liquid metals. Adv Mater Interfaces 2021;8:2001936.
25. Handschuh-wang S, Stadler FJ, Zhou X. Critical review on the physical properties of gallium-based liquid metals and selected pathways for their alteration. J Phys Chem C 2021;125:20113-42.
27. Liu J, Sheng L, He ZZ. Liquid metal soft machines: principles and applications. Singapore: Springer; 2019.
28. Yang J, Yang Y, He Z, Chen B, Liu J. A personal desktop liquid-metal printer as a pervasive electronics manufacturing tool for society in the near future. Engineering 2015;1:506-12.
29. Sheng L, Zhang J, Liu J. Diverse transformations of liquid metals between different morphologies. Adv Mater 2014;26:6036-42.
30. Zhang J, Yao Y, Sheng L, Liu J. Self-fueled biomimetic liquid metal mollusk. Adv Mater 2015;27:2648-55.
31. Wang H, Chen S, Li H, et al. A liquid gripper based on phase transitional metallic ferrofluid. Adv Funct Mater 2021;31:2100274.
32. Zhang R, Ye Z, Gao M, et al. Liquid metal electrode-enabled flexible microdroplet sensor. Lab Chip 2020;20:496-504.
33. Guo R, Sheng L, Gong H, Liu J. Liquid metal spiral coil enabled soft electromagnetic actuator. Sci China Technol Sci 2018;61:516-21.
34. Tang SY, Khoshmanesh K, Sivan V, et al. Liquid metal enabled pump. Proc Natl Acad Sci U S A 2014;111:3304-9.
35. Yang X, Tan S, Yuan B, Liu J. Alternating electric field actuated oscillating behavior of liquid metal and its application. Sci China Technol Sci 2016;59:597-603.
36. Yuan B, Tan S, Zhou Y, Liu J. Self-powered macroscopic Brownian motion of spontaneously running liquid metal motors. Sci Bull 2015;60:1203-10.
37. Zhang J, Yao Y, Liu J. Autonomous convergence and divergence of the self-powered soft liquid metal vehicles. Sci Bull 2015;60:943-51.
38. Tan S, Yuan B, Liu J. Electrical method to control the running direction and speed of self-powered tiny liquid metal motors. Proc R Soc A 2015;471:20150297.
39. Sheng L, He Z, Yao Y, Liu J. Transient state machine enabled from the colliding and coalescence of a swarm of autonomously running liquid metal motors. Small 2015;11:5253-61.
40. Nurge MA, Youngquist RC, Starr SO. Drag and lift forces between a rotating conductive sphere and a cylindrical magnet. Am J Phys 2018;86:443-52.
41. Tan S, Gui H, Yuan B, Liu J. Magnetic trap effect to restrict motion of self-powered tiny liquid metal motors. Appl Phys Lett 2015;107:071904.
42. Tan SC, Yang XH, Gui H, et al. Galvanic corrosion couple-induced Marangoni flow of liquid metal. Soft Matter 2017;13:2309-14.
43. Zhang J, Sheng L, Liu J. Synthetically chemical-electrical mechanism for controlling large scale reversible deformation of liquid metal objects. Sci Rep 2014;4:7116.
44. Redzic DV. Electromagnetostatic charges and fields in a rotating conducting sphere. Prog Electromagn Res 2010;110:383-401.
45. Jia XM. Whole-space analysis of the magnetic field of rotating sphere with charged (in Chinese). College Physics 2010; 29:20-21.
46. Jin SW, Park J, Hong SY, et al. Stretchable loudspeaker using liquid metal microchannel. Sci Rep 2015;5:11695.
47. Milde P, Köhler D, Seidel J, et al. Unwinding of a skyrmion lattice by magnetic monopoles. Science 2013;340:1076-80.
48. Dirac PAM. Quantised singularities in the electromagnetic field. Proc R Soc Lond A 1931;133:60-72.
50. Polyakov AM. Particle spectrum in quantum field theory. 30 Years of the Landau Institute - Selected Papers. WORLD SCIENTIFIC; 1996. p. 540-1.
52. Wu TT, Yang CN. Concept of nonintegrable phase factors and global formulation of gauge fields. Phys Rev D 1975;12:3845-57.
53. Abrikosov AA Jr. Dirac operator on the Riemann sphere. arXiv e-prints 2002;arXiv:hep-th/0212134.
54. Béché A, Van Boxem R, Van Tendeloo G, Verbeeck J. Magnetic monopole field exposed by electrons. Nature Phys 2014;10:26-9.
55. Fang Z, Nagaosa N, Takahashi KS, et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 2003;302:92-5.
56. Bovo L, Bloxsom JA, Prabhakaran D, Aeppli G, Bramwell ST. Brownian motion and quantum dynamics of magnetic monopoles in spin ice. Nat Commun 2013;4:1535.
59. Pietilä V, Möttönen M. Creation of Dirac monopoles in spinor Bose-Einstein condensates. Phys Rev Lett 2009;103:030401.
60. Ray MW, Ruokokoski E, Kandel S, Möttönen M, Hall DS. Observation of Dirac monopoles in a synthetic magnetic field. Nature 2014;505:657-60.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Zhou YX, Zu JS, Liu J. Insights into fluidic endogenous magnetism and magnetic monopoles from a liquid metal droplet machine. Soft Sci 2021;1:15. http://dx.doi.org/10.20517/ss.2021.16
AMA Style
Zhou YX, Zu JS, Liu J. Insights into fluidic endogenous magnetism and magnetic monopoles from a liquid metal droplet machine. Soft Science. 2021; 1(3): 15. http://dx.doi.org/10.20517/ss.2021.16
Chicago/Turabian Style
Zhou, Ying-Xin, Jia-Sheng Zu, Jing Liu. 2021. "Insights into fluidic endogenous magnetism and magnetic monopoles from a liquid metal droplet machine" Soft Science. 1, no.3: 15. http://dx.doi.org/10.20517/ss.2021.16
ACS Style
Zhou, Y.X.; Zu J.S.; Liu J. Insights into fluidic endogenous magnetism and magnetic monopoles from a liquid metal droplet machine. Soft. Sci. 2021, 1, 15. http://dx.doi.org/10.20517/ss.2021.16
About This Article
Copyright
Data & Comments
Data
 Cite This Article 22 clicks
Cite This Article 22 clicks













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.