Control of low dimensionality in flexible hybrid inorganic-organic superlattices
Abstract
The control of electron and phonon transport by manipulating dimensionality is essential for the performance of advanced electronic materials and devices, such as quantum electronics, thermoelectrics and superconductors, which may also lead to yet undiscovered, emergent electronic or thermal phenomena. In this study, we report a series of hybrid inorganic-organic superlattice structures, in which metallic TiS2 monolayers are spatially confined between soft and insulating organic molecules of varying thicknesses. By choosing different organic molecules that increase the interlayer distance, the electrons inside the TiS2 layers gradually become two-dimensional, with increasing density of states, as seen by their effective mass that increases from 5.3 to 8.6 m0, where m0 is the mass of a bare electron. In addition, density functional theory calculations confirm a transition of the electron distribution from bulk to two-dimensional, due to the suppressed interlayer coupling. This result demonstrates that the thermoelectric transport of two-dimensional electrons can be realized in a three-dimensional inorganic-organic superlattice, thus enabling access to the interesting properties of individual two-dimensional materials in the bulk form, which may provide new opportunities in flexible thermoelectrics.
Keywords
INTRODUCTION
The emergence and popularity of two-dimensional materials (2D) have opened up new opportunities for achieving superb thermoelectric properties compared with their bulk counterparts, as evidenced by tremendous theoretical predictions and some experimental reports[1-8]. However, as the thickness of individual 2D materials is restricted to a few atoms, the maximum heat and current loads allowed through the devices are severely limited, which are not practical for macroscopic thermoelectric applications with energy conversion power at the level of watts. Although there have been many efforts to integrate 2D materials into thick films or three-dimensional (3D) structures, fabrication techniques might introduce undesired doping and defects that compromise electronic properties and lead to the disappearance of the 2D states and their superb properties[9-11]. Realizing the promising thermoelectric properties of 2D materials in a 3D bulk structure is strongly desired for their practical integration into thermoelectric devices with large thermal and electrical loads.
There have been several strategies to realize 2D electronic states in a bulk structure. It was proposed by Hicks and Dresselhaus[12] that confining a conducting thin layer inside insulating layers can result in 2D electrons. The density of states increased, leading to a high Seebeck coefficient and likely an improved thermoelectric performance[12]. This concept was later validated by the observation of the giant Seebeck coefficient in SrTiO3/SrTi0.8Nb0.2O3 superlattices, where a 2D electron gas (2DEG) can be formed at the interfaces[13]. In contrast, by confining electrons into 2DEGs in GaN/AlN/Al0.2Ga0.8N superlattices, the electron mobility can be greatly enhanced to achieve an improvement in ZT[14]. Meanwhile, 2D materials have been widely recognized to provide a platform in which unconventional pairing states appear in the high-temperature superconductors of layered WTe2[15] and FeSe[16]. Furthermore, dimensionality-tuned properties have been demonstrated in these layered compounds, with distinctively different critical temperatures Tc being observed in structures with different interlayer spacings[17,18]. Intuitively, a crossover of the transport regime from 3D to 2D can be expected, if the interlayer spacing is changed. Such dimensionality crossover leads to the discovery of novel superconductors, like NaxCo2O4·yH2O, where water molecules are inserted between conducting CoO2 layers[19]. In addition to the effective control of electron transport, phonon transport can also be tailored by dimensionality crossover. Low-dimensional structures appear to have the ability to focus phonons along particular directions leading to ultra-low thermal conductivity[20,21], as well as unusually high thermal conductivity[22].
In our previous work, we studied the thermoelectric properties of bulk inorganic-organic superlattices, in which the inorganic conducting layers were spatially separated by insulating organic layers[23]. Enhanced thermoelectric properties were discovered, together with superior mechanical flexibility. However, 2D electron states and superior thermoelectric properties were not obtained in the hybrid system, as the interlayer distance was limited to 9.65 Å and the interlayer coupling interaction was not decoupled. In this study, by choosing organic molecules of different sizes through a chemical solvent exchange process, the distance between the neighboring inorganic layers is modulated and the insulating organic component can become an electrostatic barrier that confines the electrons inside the inorganic layers. Such intercalation leads to a quantum well structure and 2D transport of charge carriers can be realized in inorganic layers. This dimensionality control is demonstrated by the change in the effective mass of electrons, as well as the electron density distribution as a function of the interlayer distance. Although thermoelectric ZT has not been optimized, this study demonstrates that dimensionality crossover can be achieved in a 3D bulk material, thereby enabling access to the interesting properties of individual 2D materials in the bulk form, which may provide new opportunities in flexible thermoelectrics.
EXPERIMENTAL
We developed an electrochemical processing technique that can be used to synthesize a superlattice structure inside a bulk single crystal. This process opens up the van der Waals gap of a layered material, like TiS2, through an electrochemical reaction, followed by ion exchange or solvent exchange to diversify and tune the composition.
TiS2 single crystals with typical dimensions of 4 mm × 4 mm × 100 μm were grown by the chemical vapor transport method using excess sulfur as the transport agent. The hybrid inorganic-organic superlattice compositions were then prepared using an electrochemical process. A TiS2 single crystal and a platinum plate were used as the cathode and anode, respectively. A solution of hexyl amine (HA) hydrochloride dissolved in dimethyl sulfoxide (DMSO) was used as the electrolyte. The electrochemical reaction was performed under a voltage of 1.8 V for 20 min. Some of the Ti4+ ions were reduced to Ti3+. The TiS2 layer was therefore negatively charged and the positive organic cation in the electrolyte was driven by the Coulombic force. After the intercalation, the thickness of TiS2 increased to 2.5 times the original thickness. Simultaneously, the uncharged solvent molecules entered the superlattice together due to the cation-dipole effect. The as-synthesized TiS2/HA/DMSO was then treated in glycerin and H2O overnight for solvent exchange and cation transfer, respectively. The thickness decreased by ~30% after the solvent exchange with water.
The fabricated hybrid material was then analyzed with X-ray diffraction (XRD) and high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM). The transport properties of the samples were measured with homemade apparatuses. The Seebeck coefficient was obtained from the slope of the thermovoltage versus temperature gradient. The electrical conductivity was measured by the van der Pauw method. The thermal conductivity was obtained by using the parallel conductance method[24]. All the measurements were calibrated using some reference samples, such as TiS3 and Mg2Si, with accuracies within 5%. All the samples were fabricated independently and measured twice or three times to ensure the repeatability of the results. The Hall coefficient was measured using the van der Pauw technique under a reversible magnetic field of 0.5 T (ResiTest8300, Rigaku). The cross-plane thermal conductivity was obtained by multiplying the thermal diffusivity measured by the laser flash analysis method, the heat capacity measured by differential scanning calorimetry and the density calculated by mass over volume.
RESULTS AND DISCUSSION
Chemical and structural analysis of inorganic-organic superlattices
The TiS2 single crystal is a typical layered transition metal dichalcogenide with a trigonal space group (P-3m1), consisting of a Ti layer sandwiched between two layers of S atoms in an octahedral configuration[25]. Each three-atom slab is stacked with its neighboring layers via relatively weak van der Waals interactions. The prepared hybrid material maintained the same basal plane as that of the TiS2 single crystal but was expanded along the c-axis. Different from the brittle pristine TiS2 single crystal, the hybrid superlattices became soft and flexible. For instance, a 54-μm-thick TiS2/HA/DMSO superlattice sample can still maintain a resistance change of no more than 2% when the bending radius is 2 mm [Supplementary Figure 1].
Structural analysis of the hybrid materials demonstrated the increase of the lattice constant in the c-axis direction, namely, the interlayer distance between the TiS2 monolayers. The most obvious evidence for the expansion of the interlayer distance came from XRD. The shift of the (00l) peaks reflected the change of the interlayer distance. The (001) peak of bulk TiS2 is located at 15.5°, corresponding to an interlayer distance of 5.9 Å (as shown in Figure 1A). After the intercalation of the organic molecules, all of the (001) peaks shifted to lower angles.
Figure 1. Crystal structures of a TiS2 single crystal and the hybrid inorganic-organic superlattices with different interlayer distances. (A) TiS2 single crystal. (B) HAADF-STEM image of TiS2/HA/H2O. (C) TiS2/HA/H2O. (D) TiS2/HA/DMSO corresponding to the 1D electron density map along the c-axis. (E) TiS2/HA/glycerin corresponding to the 1D electron density map along the c-axis.
Despite the fact that the same intercalant (HA) was used, we find that the interlayer distance and thermal stability of the superlattice structures are sensitive to the solvent. When different solvent molecules were exchanged into the superlattices, the corresponding interlayer distance changed accordingly
We thus examined the structure of the most stable compound TiS2/HA/H2O using HAADF-STEM. As shown in Figure 1B, the bright points represent the inorganic TiS2 layer and the interlayer distance is measured to be 9.65 Å, consistent with the XRD results. The dark area is filled with organic molecules, which support the gaps between inorganic layers. Therefore, the superlattice structure of hybrid inorganic-organic material is confirmed by the HAADF-STEM imaging showing a clear alternating stacking pattern of TiS2 and organic layers (as shown in Figure 1C).
For the other compositions, TiS2/HA/DMSO and TiS2/HA/glycerin, which have lower stability and cannot be observed by HAADF-STEM, the stacking structure of the inorganic-inorganic superlattices can be analyzed with the one-dimensional (1D) electron density map along the c-axis. The 1D electron density maps are derived from the Fourier transform of the XRD results (see supplementary material), as shown in Figures 1D and E. Three sharp peaks located at -1.4, 0 and 1.4 Å represent the triple atomic planes in TiS2. The organic molecules in the interlayer spacing contributed to the small peaks appearing between the neighboring strong triple peaks, indicating relatively ordered spatial arrangements. The similar peaks next to the triple peaks by 1.4 Å appeared in all the electron density maps, which should belong to the ammonium head groups of HA cations. There are also some relatively strong symmetric peaks located in the interlayer space of the superlattices. These peaks are attributed to the electronegative oxygen and sulfur atoms in the neutral polar molecules, such as DMSO and glycerin, exchanged into the superlattice. Through the cation-dipole effect, they were also regularly arranged between the inorganic layers.
With different sizes of the intercalated molecules, we have demonstrated that the interlayer distance is controllable, indicating excellent opportunities for tunable thermal, electronic and thermoelectric properties. In the following sections, detailed experimental characterization and theoretical analysis are described to demonstrate the dimensionality-controlled thermoelectric transport properties.
Electrical transport properties of inorganic-organic superlattices
The transport properties of TiS2 single crystal and the hybrid inorganic-organic superlattices were measured, as shown in Table 1. As a result of the high density of electronic states (mainly composed of the three-fold degenerate t2g orbitals of the 3d electrons of the Ti atom) around the Fermi level, TiS2 showed a high Seebeck coefficient and power factor[26]. The transport properties strongly depended on the growth conditions, which might induce nonstoichiometry (interstitial Ti atoms) and other defects[27]. We grew TiS2 single crystal using excess sulfur rather than conventional iodine as a transport agent to avoid impurities. The obtained TiS2 single crystals show a Seebeck coefficient of -160 μV K-1, which was lower than that of the nearly stoichiometric sample, because of the extra electrons donated by the interstitial Ti atoms. The Hall measurements showed a carrier concentration of 3.4 × 1020 cm-3. Assuming that each interstitial Ti atom contributes four electrons, the actual composition of the single crystals was calculated to be Ti1.0049S2.
Electrical transport properties of TiS2 single crystals and the hybrid inorganic-organic superlattices
| Compositions | Td | In-plane properties | Cross-plane properties | |||||
| S | σ | n | μ | m* | σ | |||
| TiS2 | ~ | -160 | 409 | 3.40 | 7.24 | 5.3 | 0.51 | |
| A | 40 | -75 | 363 | 8.48 | 2.67 | 8.3 | 0.14 | |
| B | 70 | -75 | 534 | 9.11 | 3.66 | 8.6 | 0.16 | |
| C | 120 | -78 | 781 | 7.59 | 6.41 | 6.2 | 2.73 | |
After the intercalation of HA ions, the Seebeck coefficient became -75 μV K-1 and the electrical conductivity became 363 S cm-1 at room temperature. During the electrochemical process, the TiS2 layers were electrochemically reduced, so the carrier concentration in the TiS2 layers increased and was equal to the density of the intercalated organic cations according to the requirement of charge neutrality. The Hall measurements demonstrated that the carrier concentration increased to 8.48 × 1020 cm-3. Meanwhile, the mobility became 2.67 cm2 V-1 s-1, which was reduced compared with that of the TiS2 single crystal. Since the electrons were primarily localized within the TiS2 layers and the conduction pathway was well preserved, there should be minimal additional scattering in the inorganic-organic superlattice. The electrons in pure TiS2 were mainly scattered by acoustic phonons[28], where the electron effective mass also played an important role. In this quantum well system, the electron effective mass may be changed, which will be analyzed later.
The incorporation of neutral glycerin molecules almost barely changed the concentration of the organic cations (HA ions) and therefore should not influence the electron density in the TiS2 layers. The electrical conductivity increased from 363 to 534 S cm-1. The Hall measurements showed that this increase was mainly due to an increase in mobility. The polar glycerin molecules with a relatively high dielectric constant in the van der Waals gap of TiS2 may help screen the deformation potential induced by the lattice vibrations of the TiS2 layers, which decreased the acoustic phonon scattering effect and enhanced the electron mobility[29].
For the TiS2/HA/H2O case, with the highest thermal stability among the three different materials, the Seebeck coefficient exhibits a slight improvement in comparison with the two previous samples. The electrical conductivity was much larger in comparison with the previous two samples. The Hall measurements confirmed that the carrier concentration only slightly decreased, possibly because of a loss of organic cations during the ion exchange process, which can reduce the corresponding negative electron density in the inorganic TiS2 layers. Meanwhile, the mobility increased to a value close to that of the pristine TiS2 single crystal.
2D electron transport in inorganic-organic superlattices
Since the intercalated molecules are insulating, the electron pathway is predominantly inside the inorganic TiS2 layers, likely confined inside the TiS2 monolayers and determined by the scattering processes inside each TiS2 layer[28]. Using the volume fraction of the inorganic component derived from the interlayer distance measured by XRD, the real carrier concentration inside the TiS2 layers can be estimated. The effective mass m* can then be deduced from the Seebeck coefficient S and the carrier concentration n[30]:
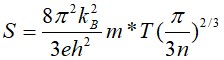
The results show that the effective mass of all the inorganic-organic superlattices increased from that of the pristine TiS2 single crystal, as shown in Figure 2A. The TiS2 layers are spatially confined between the insulating organic molecules, which can behave as electrostatic potential barriers. A 2DEG could form inside the TiS2 layers, which increased the density of states at the edge of the conduction band and enhance the effective mass. As shown in Figure 2A, the dimensionality crossover is evidenced by the continuously increased effective mass and decreased mobility with the expanding interlayer distances[31]. Since the insulating organic molecules filling the van der Waals gaps have a much wider bandgap than TiS2, they can be considered as potential barriers that separate the conducting TiS2 layers that resemble 2D potential wells. With larger interlayer distances, the width of the potential barriers also increases; hence, the interlayer electron transport is suppressed, resulting in an increased effective mass and decreased mobility. Ultimately, a large spacing leads to a stack of effectively isolated TiS2 monolayers. Our previous work calculated the electronic structure of the TiS2 monolayer, in which electrons are completely confined two-dimensionally and the effective mass is doubled compared with the bulk value[1]. The observed increased effective mass from 5.3 m0 for single crystal TiS2 to 8.3 m0 for TiS2/HA/DMSO with a large interlayer spacing of 13.97 Å suggests we almost approach the monolayer limit.
Figure 2. Demonstration of the gradual two-dimensionalization of electrons with increasing interlayer distance. (A) Effective mass and mobility in the in-plane direction as a function of interlayer distance. (B) Temperature dependence of the cross-plane electrical conductivity of the hybrid organic-inorganic superlattices, in which (a-d) represent the TiS2 single crystal,
The formation and the tunability of the 2DEG are also manifested in the temperature dependence of electric conductivity, as shown in Figure 2B. The inorganic-organic superlattices have a highly anisotropic electrical conductivity and the cross-plane electrical conductivities are ~800-2000 times lower than the in-plane values, which can be explained by regarding the organic layers as potential barriers that suppress interlayer charge transport. In addition, the temperature dependence of electrical conductivity for TiS2/HA/DMSO (d = 13.97 Å) and TiS2/HA/glycerin (d = 13.84 Å) is much weaker than the pristine TiS2 and TiS2/HA/H2O with smaller interlayer distances. With large widths and heights of potential barriers formed by DMSO and glycerin molecules, the tunneling process dominating the interlayer electron transport is suppressed. In contrast, TiS2/HA/H2O has a short interlayer distance and hence the potential barrier is much narrower, resulting in the stronger coupling of charge carriers between neighboring TiS2 layers and a metallic electrical conductivity in the cross-plane direction. The temperature dependence of electrical conductivity in
In addition to the experimental characterization, we also performed density functional theory (DFT) calculations to provide theoretical insights into the confinement of electron gas inside TiS2 monolayers by changing the interlayer distances. We calculated the electronic density of states (DOS) of the conduction band as a function of the interlayer distance of TiS2, as shown in Figure 3. For bulk TiS2, the DOS at the conduction band edge showed a gradual increase, but the DOS of the monolayer TiS2 experiences a sharp increase at the band edge, which is a typical feature for a 2DEG. For the structure with intermediate interlayer distances (9.65 and 13.90 Å), the slope of the DOS at the band edge is between the bulk TiS2 and single layer TiS2. This DOS clearly showed a bulk-to-2D transition of the electronic structure.
We can also visualize such a transition in the electron distribution from 3D to 2D by calculating the valence electron distributions [Figures 4A-D]. In bulk TiS2, the electron density clouds of different TiS2 layers overlap with each other to form a 3D distribution. However, the electrons in each monolayer become decoupled from the neighboring layers when the interlayer distance increases. Our DFT simulations of the DOS and the spatial electron density distribution indicate that increasing the van der Waals gap between the TiS2 layers can suppress the interlayer coupling and the electron transport in these intercalated compounds gradually becomes 2D-like.
Thermoelectric performance as a function of interlayer distance
It is important to realize that careful control of the interlayer spacing is important to avoid excessive reduction of the electrical conductivity that compromises the thermoelectric performance. While opening the van der Waals gaps between TiS2 layers can enhance the effective mass of electrons, it does not always improve the power factor, because the loss in mobility could counterbalance the gain in the Seebeck coefficient. In addition, the large volume fraction of the insulating organic molecules also decreases the electrical conductivity.
In addition to the electrical properties, increasing the van der Waals gap by organic molecule intercalation can result in much lower phononic thermal conductivities and thereby an enhanced ZT value. Through the parallel thermal conductance method, the thermal conductivity of the pristine TiS2 single crystal was measured to be 4.45 W m-1 K-1 along the in-plane direction. The corresponding values for TiS2/HA/DMSO, TiS2/HA/glycerin and TiS2/HA/H2O were measured to be 0.76, 0.83 and 0.69 W m-1 K-1, respectively, which were about six times lower than that of the starting TiS2 single crystal [Table 2].
Thermal transport and thermoelectric properties of TiS2 single crystal and the hybrid inorganic-organic superlattices
| Compositions | Cross-plane properties | In-plane properties | |||||
| κ | κL | S2σ | κ | κL | ZT | ||
| TiS2 | 1.92 | 1.92 | 1.05 | 4.45 | 4.24 | 0.07 | |
| A | 0.50 | 0.50 | 0.20 | 0.76 | 0.54 | 0.08 | |
| B | 0.49 | 0.49 | 0.30 | 0.83 | 0.51 | 0.11 | |
| C | 0.11 | 0.11 | 0.48 | 0.69 | 0.22 | 0.21 | |
As the thermal conductivity is contributed to by both phonons and electrons, the Wiedemann-Franz law was used to estimate the electronic thermal conductivity[32]. The lattice thermal conductivity of the TiS2 single crystal was calculated to be 4.24 W m-1 K-1 and the values for the three compositions become 0.22-0.54 W m-1 K-1, which were significantly lower than the value of TiS2. The huge reduction of the thermal conductivity from pure TiS2 to the hybrid materials is because of the interaction between TiS2 and the dangling organic molecules, which provides extra scattering channels for TiS2 vibrational modes, as shown in our previous work using molecular dynamics simulations[23]. Meanwhile, the thermal conductivity of
Figure 5. In-plane thermoelectric properties of TiS2 and the hybrid inorganic-organic superlattices as a function of interlayer distance.
The cross-plane thermal conductivity was measured using the laser flash method. The electronic thermal conductivity can be neglected compared with the lattice thermal conductivity because of the low cross-plane electrical conductivity. As shown in Table 2, TiS2 shows anisotropy of thermal conductivity due to the anisotropic bonding strengths: strong covalent bonding inside the layers and weak van der Waals force between the layers. However, this anisotropy ratio between in-plane and cross-plane thermal conductivity decreased after the organic molecule intercalation. This could be attributed to the increased scattering rates of vibrational modes inside TiS2 due to the anharmonic coupling with the organic molecules, which was demonstrated by molecular dynamics simulations in our previous work[23].
CONCLUSIONS
In summary, we presented a series of materials with a hybrid organic-inorganic superlattice structure, in which the inorganic conducting TiS2 layers are spatially confined between soft organic molecules. The interlayer distance was systematically tuned by different organic molecules from 9.65-13.96 Å. Gradual dimensional crossover of the electrons from 3D to 2D was demonstrated with increasing interlayer distance, which was evidenced by the increase of effective mass from 5.6 to 8.3 m0. Meanwhile, the electron distribution was analyzed through DFT calculations, which confirm the dimensional crossover of electrons with increasing interlayer distance.
Atomically thin 2D materials show excellent potential in thermoelectric energy conversion due to their superb electronic properties, but the higher thermal conductivities of 2D materials could lead to a low thermoelectric figure of merit[33]. The result demonstrates that thermoelectric transport of 2D electrons can be realized in a 3D inorganic-organic superlattice, thus enabling access to the interesting properties of individual 2D materials in the bulk form, which may provide new opportunities in flexible thermoelectrics. Many other layered materials, such as Bi2Te3 and the transition metal dichalcogenides NbS2, TaS2, VS2, CrS2, MoS2 and WSe2, can be intercalated to make both n- and p-type inorganic-organic superlattices materials and realize potentially high thermoelectric properties.
DECLARATIONS
Authors’ contributionsWrote and reviewed the manuscript: Yin SJ, Qian X, Koumoto K, Yang RG, Wan CL
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by the China Key National R&D Plan (No. 2017YFA0700705) and the National Natural Science Foundation of China (No. 51788104 and No. 51590893).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
Supplementary Materials
REFERENCES
1. Zhang RZ, Wan CL, Wang YF, Koumoto K. Titanium sulphene: two-dimensional confinement of electrons and phonons giving rise to improved thermoelectric performance. Phys Chem Chem Phys 2012;14:15641-4.
2. Huang W, Luo X, Gan CK, Quek SY, Liang G. Theoretical study of thermoelectric properties of few-layer MoS2 and WSe2. Phys Chem Chem Phys 2014;16:10866-74.
3. Hippalgaonkar K, Wang Y, Ye Y, et al. High thermoelectric power factor in two-dimensional crystals of $\mathrm{Mo}{\mathrm{S}}_{2}$. Physical Review B 2017;95:115407.
4. Wu J, Chen Y, Wu J, Hippalgaonkar K. Perspectives on thermoelectricity in layered and 2D materials. Advanced Electronic Materials 2018;4:1800248.
5. Kayyalha M, Maassen J, Lundstrom M, Shi L, Chen YP. Gate-tunable and thickness-dependent electronic and thermoelectric transport in few-layer MoS2. Journal of Applied Physics 2016;120:134305.
6. Pallecchi I, Manca N, Patil B, Pellegrino L, Marré D. Review on thermoelectric properties of transition metal dichalcogenides. Nano Futures 2020;4:032008.
7. Shimizu S, Shiogai J, Takemori N, et al. Giant thermoelectric power factor in ultrathin FeSe superconductor. Nat Commun 2019;10:825.
8. Cao YD, Sun YH, Shi SF, Wang RM. Anisotropy of two-dimensional ReS2 and advances in its device application. Rare Metals 2021.
9. Novak TG, Kim K, Jeon S. 2D and 3D nanostructuring strategies for thermoelectric materials. Nanoscale 2019;11:19684-99.
10. Huang H, Cui Y, Li Q, et al. Metallic 1T phase MoS2 nanosheets for high-performance thermoelectric energy harvesting. Nano Energy 2016;26:172-9.
11. Li D, Gong Y, Chen Y, et al. Recent progress of two-dimensional thermoelectric materials. Nanomicro Lett 2020;12:36.
12. Hicks LD, Dresselhaus MS. Effect of quantum-well structures on the thermoelectric figure of merit. Phys Rev B Condens Matter 1993;47:12727-31.
13. Ohta H, Kim S, Mune Y, et al. Giant thermoelectric Seebeck coefficient of a two-dimensional electron gas in SrTiO3. Nat Mater 2007;6:129-34.
14. Sztein A, Bowers JE, DenBaars SP, Nakamura S. Polarization field engineering of GaN/AlN/AlGaN superlattices for enhanced thermoelectric properties. Applied Physics Letters 2014;104:5.
15. Zhang H, Rousuli A, Shen S, et al. Enhancement of superconductivity in organic-inorganic hybrid topological materials. Science Bulletin 2020;65:188-93.
16. Shi MZ, Wang NZ, Lei B, et al. FeSe-based superconductors with a superconducting transition temperature of 50 K. New Journal of Physics 2018;20:123007.
17. Harshman DR, Mills AP Jr. Concerning the nature of high-Tc superconductivity: Survey of experimental properties and implications for interlayer coupling. Phys Rev B Condens Matter 1992;45:10684-712.
18. Burrard-Lucas M, Free DG, Sedlmaier SJ, et al. Enhancement of the superconducting transition temperature of FeSe by intercalation of a molecular spacer layer. Nat Mater 2013;12:15-9.
19. Takada K, Sakurai H, Takayama-Muromachi E, Izumi F, Dilanian RA, Sasaki T. Superconductivity in two-dimensional CoO2 layers. Nature 2003;422:53-5.
20. Qian X, Zhou J, Chen G. Phonon-engineered extreme thermal conductivity materials. Nat Mater 2021;20:1188-202.
21. Huang Y, Wan C: Controllable fabrication and multifunctional applications of graphene/ceramic composites. Journal of Advanced Ceramics 2020;9:271-91.
22. Xu X, Chen J, Zhou J, Li B. Thermal conductivity of polymers and their nanocomposites. Adv Mater 2018;30:e1705544.
23. Wan C, Gu X, Dang F, et al. Flexible n-type thermoelectric materials by organic intercalation of layered transition metal dichalcogenide TiS2. Nat Mater 2015;14:622-7.
24. Zawilski BM, Littleton RT, Tritt TM: Description of the parallel thermal conductance technique for the measurement of the thermal conductivity of small diameter samples. Review of Scientific Instruments 2001;72:1770-4.
25. Fang CM, de Groot RA, Haas C. Bulk and surface electronic structure of 1T-TiS2 and 1T-TiSe2. Physical Review B 1997; 56:4455-63.
26. Imai H, Shimakawa Y, Kubo Y. Large thermoelectric power factor in TiS2 crystal with nearly stoichiometric composition. Physical Review B 2001;64:241104.
27. Barry JJ, Hughes HP, Klipstein PC, Friend RH. Stoichiometry effects in angle-resolved photoemission and transport studies of TI1+XS2. Journal of Physics C-Solid State Physics 1983;16:393-402.
28. Wan C, Wang Y, Wang N, Norimatsu W, Kusunoki M, Koumoto K. Intercalation: building a natural superlattice for better thermoelectric performance in layered chalcogenides. Journal of Electronic Materials 2011;40:1271-80.
29. Cardona M, Christensen NE. Acoustic deformation potentials and heterostructure band offsets in semiconductors. Phys Rev B Condens Matter 1987;35:6182-94.
31. Ohta H, Mune Y, Koumoto K, Mizoguchi T, Ikuhara Y. Critical thickness for giant thermoelectric Seebeck coefficient of 2DEG confined in SrTiO3/SrTi0.8Nb0.2O3 superlattices. Thin Solid Films 2008;516:5916-20.
32. Kim H-S, Gibbs ZM, Tang Y, Wang H, Snyder GJ. Characterization of Lorenz number with Seebeck coefficient measurement. APL Materials 2015:3.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Yin S, Qian X, Koumoto K, Yang R, Wan C. Control of low dimensionality in flexible hybrid inorganic-organic superlattices. Soft Sci 2021;1:9. http://dx.doi.org/10.20517/ss.2021.10
AMA Style
Yin S, Qian X, Koumoto K, Yang R, Wan C. Control of low dimensionality in flexible hybrid inorganic-organic superlattices. Soft Science. 2021; 1(2): 9. http://dx.doi.org/10.20517/ss.2021.10
Chicago/Turabian Style
Yin, Shujia, Xin Qian, Kunihito Koumoto, Ronggui Yang, Chunlei Wan. 2021. "Control of low dimensionality in flexible hybrid inorganic-organic superlattices" Soft Science. 1, no.2: 9. http://dx.doi.org/10.20517/ss.2021.10
ACS Style
Yin, S.; Qian X.; Koumoto K.; Yang R.; Wan C. Control of low dimensionality in flexible hybrid inorganic-organic superlattices. Soft. Sci. 2021, 1, 9. http://dx.doi.org/10.20517/ss.2021.10
About This Article
Copyright
Data & Comments
Data

 Cite This Article 17 clicks
Cite This Article 17 clicks

















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.