Uncovering isolated resonant responses in antagonistic pure-shear dielectric elastomer actuators

System overview and actuation principle

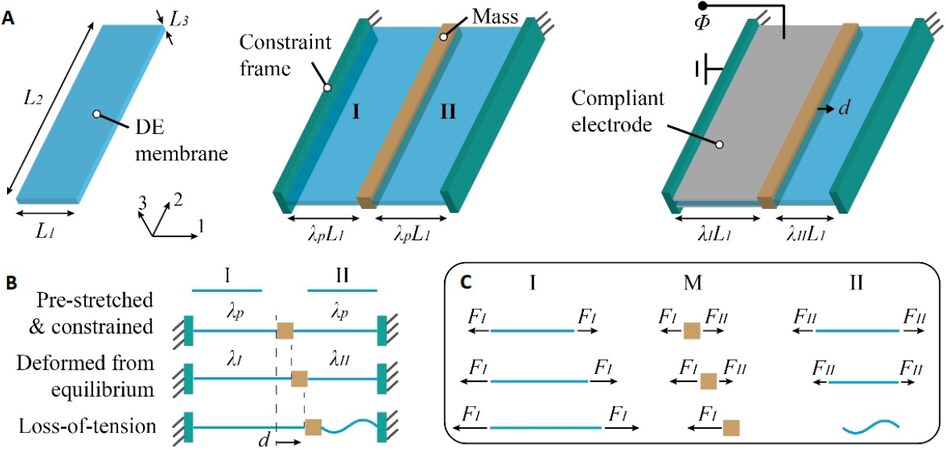
The basic structure of the antagonistic pure-shear DEA is shown in Figure 1A. The undeformed DE membrane has the dimensions of L₁, L₂, and L₃ in direction 1, 2, and 3, respectively. Two identical DE membranes, I and II, are pre-stretched along direction 1 by λ_p and then bonded to the constraint frames. One mass, M, is attached to one end of each membrane and is constrained to allow only horizontal translation (i.e., no vertical motion, hence neglecting gravitational force). In its passive equilibrium (no actuation voltage applied), the mass is balanced in the center by the tensile forces of the two membranes, F_I and F_II. The actuation principle of the antagonistic pure-shear DEA relies on the force balance of the two membranes on the mass. When a voltage, Φ, is applied across the electrodes of DEA I, the electrostatic pressure, induced by the electric field, reduces the tension on membrane I, F_I. The force imbalance leads to a translation of the mass along direction 1 until another force balance is achieved between the two membranes, as is shown in Figure 1A. The stretch ratios of membranes I and II during deformation, λ_I and λ_II, are defined as the ratios of the deformed lengths in direction 1 and the initial length, L₁.

Figure 1. (A) Schematic diagram of the antagonistic pure-shear DEA and its actuation principle. (B) Demonstration of loss-of-tension in the membrane induced by large deformation (λ < 1). (C) Force balance analysis on membrane I, mass M, and membrane II.

Equation of motion

The equation of motion that describes the dynamic responses of this system has been described in detail in previous studies^{[24,26,36,40,43]}. Hence, in this work, the development of the equation of motion is introduced briefly and the final equation used for the rest of the study is given in the end of this subsection.

The two DE membranes and mass are considered separately at this stage with the subsystem membrane I being investigated first. A thermodynamic framework is adopted, which indicates that the variation of the free energy of the DE during actuation is equal to the work done jointly by the voltage, tensile force, the viscous damping, and the inertial force of the membrane.

To derive this model, it is assumed that a voltage, T_I, is applied across the compliant electrodes of the membrane and a charge, Q_I, is built on the electrodes. A tensile force, P, is applied to the membrane in direction 1. The membrane material is assumed to have a density, ρ, and a viscous damping coefficient, c. For an infinitesimal variation of δλ_I, by conservation of energy

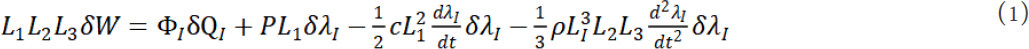
where W is the Helmholtz free energy density, and can be expressed using the Gent model^[44] as

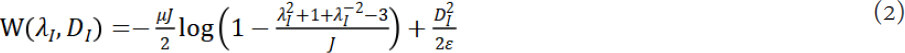
where μ is the shear modulus of the material, J is the constant relating to the limiting stretch, D_I is the electric displacement of membrane I and is given as 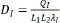, and ε is the permittivity.

Note that the Helmholtz free energy density equation given here is simplified due to there being no stretch in direction 2 on the DE membrane.

By partially differentiating equation 2 with respect to λ_I and substituting to equation 1, one can obtain the expression for the tensile force, which is written as

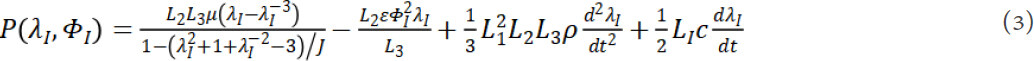
It is worth noting that a membrane is a type of element that can only withstand tension in direction 1 by neglecting the effects of shear stress in the membrane due to the sufficiently high area-to-thickness ratio. Hence if the tensional force on the membrane in the deformation direction becomes zero, the membrane loses tension in this direction, as illustrated in Figure 1B and C. However, this phenomenon cannot be captured by the well-developed continuous force-stretch function in equation 3, for instance, when λ_I < 1, the tensile force, P, becomes a finite negative value, which cannot be true. Note that in previous antagonistic pure-shear DEA studies, P was considered as a continuous function in the region-of-interest as the pre-stretch value was usually sufficiently large so that λ_I remains > 1. However, in this study, where a low pre-stretch value is used, the deformation, particularly at high-amplitude vibrations near the resonance of the system, can be large enough to cause loss-of-tension on the DE membrane which creates non-smoothness in the force function thus discontinuity in the stiffness. To take this effect in to account, a piecewise force function is used in this work, and is written as

where F_I is the true tensile force in membrane I.

Due to the constraint applied to the two DE membranes, the stretch of membrane II can be written as

Then the true tensile force, FII, can be obtained by substituting equation 5 into 4, and is given as

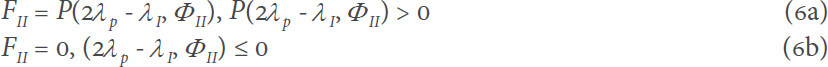
where Φ_II, is the voltage applied to membrane II.

The equation of motion for the mass can be obtained as

By performing nondimensionalization and neglecting the inertia force of the membranes by assuming a sufficiently large M compared to the mass of the membrane, ρL₁L₂L₃, the equation of motion can be rewritten as

where

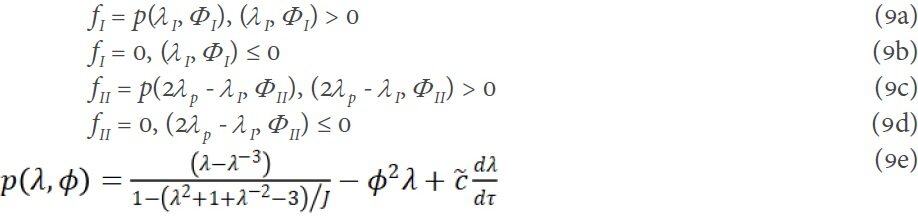
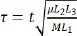is the non-dimensional time, 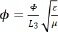is the non-dimensional voltage, is the non-dimensional damping coefficient.

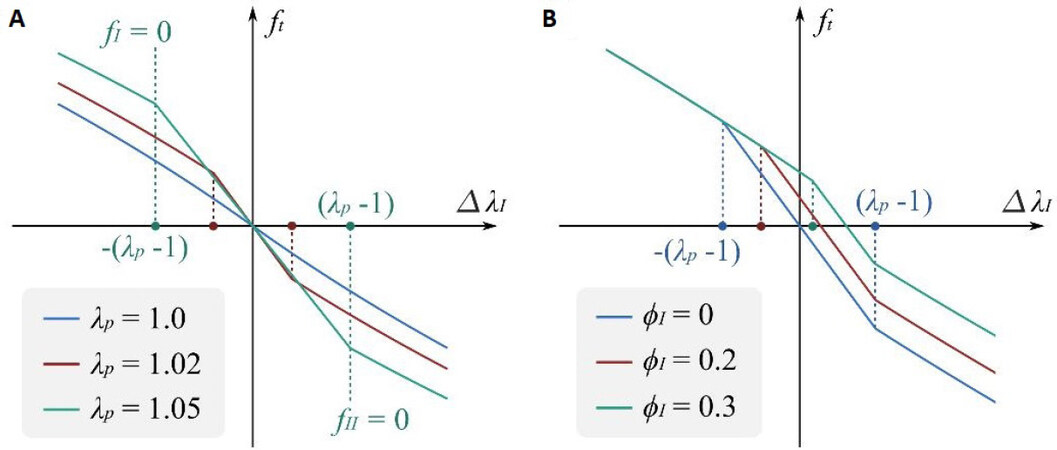
Figure 2A shows examples of the total force exerted on the mass, f_t= -f_I + f_II, against the stretch offset from its passive equilibrium (with no actuation voltage), Δλ_I = λ_I - λ_p. Note from Figure 2A that, as the pre-stretch is greater than 1.0, discontinuity is created when either f_I or f_II becomes zero, which corresponds to λ_I and λ_II = 1, respectively. It is noteworthy that, in the region where -(λ_p - 1) < Δλ_I < (λ_p - 1), the system appears to be “stiffer” (the slope is steeper) than other regions as the two membranes act on the mass antagonistically in this region. As a voltage is applied to membrane I, the discontinuity points do not necessarily correspond to λ_I and λ_II = 1, as illustrated in Figure 2B. It can be noted that the leftmost discontinuity is shifting to the right as the voltage increases and the force-displacement function is no longer symmetrical around the passive equilibrium (origin in Figure 2).

Figure 2. Force-displacement relationship of the antagonistic pure-shear DEA. (A) Total force vs. stretch offset with pre-stretch λ_p = 1.0, 1.02, and 1.05. φ_I = φ_II = 0 in all three cases. (B) Total force vs. stretch offset with non-dimensional voltage φ_I = 0, 0.2, and 0.3. λ_p = 1.02 and φ_II = 0 in all three cases.

In this work, the Gent model parameters (μ and J) are determined based on the previous studies on the silicone elastomer ELASTOSIL (Wacker Chemie AG)^[42,45,46] and is given as μ = 400 kPa and J = 16. The dimension of the elastomer is defined as L₁ = 20 mm, L₂ = 200 mm, and L₃ = 0.1 mm. The mass M is chosen as 50 g. The permittivity, ε, is a product of the absolute permittivity of a vacuum and the relative permittivity of the dielectric elastomer and is given as ε = 2.48 × 10^-11 F/m.

By solving the nondimensionalized equation of motion, equation 8, numerically in MATLAB (MathWorks), the dynamic performance of the DEA system under parametric mechanisms of excitation is investigated systemically in the following sections.

Nonlinear dynamic responses

In this section, the nonlinear dynamic responses of the pure-shear DEA under AC voltage excitation are investigated. In this study, only membrane I is subject to a time-varying voltage excitation, while no actuation voltage is applied to membrane II. The forcing term of this system, 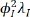, as described in equation 9e, is a function of the displacement, λ_I, hence this system is excited parametrically^[47]. It is noteworthy that the forcing term is also a function of the square of the voltage input. Therefore, for an non-dimensional AC voltage signal given as φ_I = φ_DC + φ_AC cos(ω_eτ), where φ_DC and φ_AC are the non-dimensional direct current (DC) and AC voltage amplitudes respectively and is the non-dimensional angular excitation frequency, the force experienced by the moving mass is proportional to (following the authors’ previous work^[46])

where

From equation 10 it can be noted that the voltage forcing term contains one constant biasing component and two time-varying components, one at the excitation frequency and the second at twice the input frequency. As such, when the excitation frequency is close to either the natural frequency of the DEA system or half of its value, resonances can be observed^[42,48], which are termed primary harmonic resonance and super-harmonic resonance, respectively. It is worth noting that both the DC and AC voltage amplitudes contribute to the biasing forcing component, E_a. As a result, varying either φ_AC or φ_DC could result in a change in the biasing excitation component, which then leads to a shift in the equilibrium point, and hence the resonant behavior. To analyze the dynamic responses of the DEA system consistently, the biasing forcing term, E_a, AC to DC amplitude ratio, ADR = φ_AC/φ_DC and the excitation frequency, ω_e, are considered as three independent variables. In this section, the frequency response of the DEA system is investigated by varying the excitation frequency while fixing the E_a value at 0.2², and two ADR values of 0.6 and 1.0 are chosen for comparison. In these two cases, the amplitudes for E_b are 0.041 and 0.053 respectively, while E_c is changed from 0.006 to 0.013 as ADR is increased from 0.6 to 1.0. It can be noted that, even though the biasing forcing amplitude E_a remains unchanged, the increase in ADR in fact increases the amplitudes of the two time-varying forcing components. The results of these increments will lead to a higher resonance amplitude of the DEA and can also lead to new dynamic phenomenon, as will be shown in the next subsection. The non-dimensional damping coefficient is given as and the pre-stretch ratio is λ_P = 1.02. It is noteworthy that, with the material parameters adopted in this work, the nominal electrical breakdown electric field is about 90 MV/m with no pre-stretch^[49], while the applying nominal amplitude adopted in this study is equivalent to about 40 MV/m, which is significantly lower than the critical value. As a result, it is believed that no electric breakdown occurs within this study.

Frequency sweep results

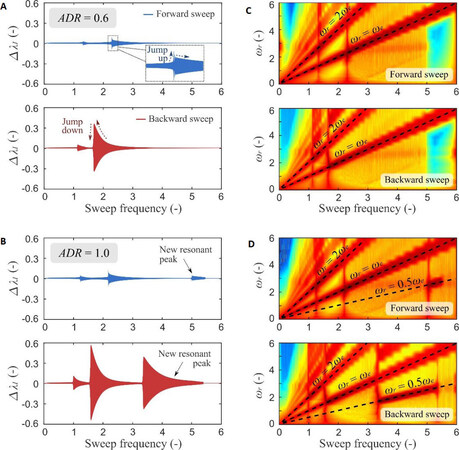
In the first study, forward and backward frequency sweeps are conducted for the ADR = 0.6 and 1.0 case from a non-dimensional frequency of 0 to 6 (6 to 0 for the backward sweep) over τ = 12000. The sweep results are shown in Figure 3A and B, respectively. For the ADR = 0.6 case, two distinct resonant peaks can be observed and, for each resonant peak, a backward sweep leads to a higher amplitude than the forward sweep, which is mainly due to the strong nonlinearity in the DEA system causing the occurrence of two possible stable oscillations at the frequencies near resonance, one with very high resonant amplitude and another one with low amplitude. Note that, in the forward frequency sweep, as the sweep frequency approaches the resonant frequency from a lower value, the response first follows the lower branch and experiences a sudden jump up, before gradually reducing as the excitation frequency increases further, as illustrated by the dark-blue arrows in Figure 3A. However, in the backward sweep result, the response follows the high amplitude branch as the sweep frequency decreases from above resonance and drops down sharply once the maximum value is reached. As the ADR value is increased to 1.0, the two resonant peaks observed in the ADR = 0.6 case grow in amplitude. Furthermore, a new resonant peak emerges at a higher sweep frequency, as marked in Figure 3B.

Figure 3. (A) Frequency sweep results of the ADR = 0.6 case, blue represents the forward frequency sweep and red illustrates the backward sweep. (B) Frequency sweep results of the ADR = 1.0 case. (C) Scalogram of the ADR = 0.6 case, where dark-red represents high-amplitude frequency responses. (D) Scalogram of the ADR = 1.0 case.

The frequency components and their amplitudes in the forward frequency sweeps for the ADR = 0.6 and 1.0 cases are analyzed using a wavelet transform and the scalograms are shown in Figure 3C and D, respectively. It can be noted from Figure 3C that the fundamental response frequency, ω_r, (the frequency component in the response with the highest amplitude, represented by the dark-red color) is equal to the excitation frequency, ω_e, with the exception near the first resonant peak, where ω_r = 2ω_e, demonstrating a super-harmonic response. The fundamental response frequency in the case ADR = 1.0 follows the same pattern. The new resonant peak found in this case shows an ω_r = 0.5ω_e relationship, which corresponds to a subharmonic response.

Detailed frequency response study

The frequency sweep results demonstrated that, apart from super-harmonic and harmonic resonance, which result from the square of the sinusoidal excitation function, there exists the subharmonic response that is not directly correlated to the excitation. The results also illustrated that multiple stable periodic solutions might exist at a single frequency for this dynamic system (e.g., the region between the jump-up and down points in Figure 3A) and the stable periodic solution of the system is determined by the its initial conditions, displacement and velocity. By using a sufficient set of initial conditions at each excitation frequency, and numerically integrating the equation of motion in the time domain until the system reaches a steady-state periodic oscillation, the stable responses of the DEA system, which might be hidden from the forward and backward sweeps, can be analyzed.

i. ADR = 0.6 case

Figure 4 shows the frequency response for the ADR = 0.6 case. It can be noted that, apart from the super-harmonic (red) and harmonic (blue) resonant peaks observed in the frequency sweep results in Figure 3A, a “hidden” resonant peak is uncovered using this multi-initial condition approach, as marked in green in Figure 4. The third resonant peak is in fact the same subharmonic resonant peak observed in the ADR = 1.0 case in Figure 3B, yet it is detached from the main response branch. Hence, in a continuous frequency sweep, such a response is not able to be captured and tends to be overlooked when analyzing such systems. Isolated response curves, or isolas, have been reported in different nonlinear dynamic systems (see, e.g.,^[50-54]). Yet to the best of the authors’ knowledge, this is the first time that an isolated subharmonic response curve being demonstrated theoretically using a parametrically forced DEA system. The mechanism leading to this type of isolated curve has not been fully understood, but it is believed to a result of the multi-valuedness of the nonlinear system at some frequencies^[50,51]. The oscillation amplitude of the isola can be over 10-fold higher than the primary response at the same frequency, once triggered, it will cause a sudden jump in the oscillation amplitude, which serves as a real threat to the dynamic stability and controllability of such DEA systems. In practical applications, this could lead to a system failure and catastrophic outcomes.

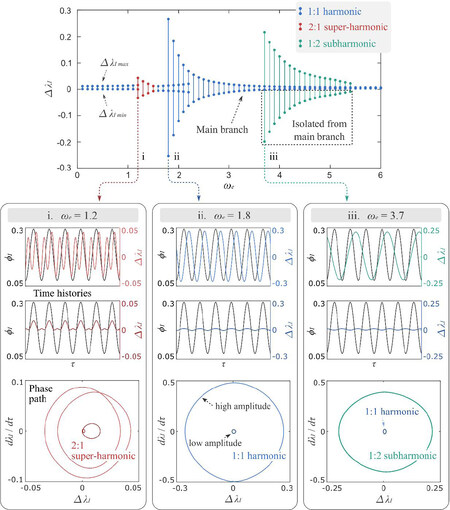
Figure 4. Frequency response, time histories and phase paths at ω_e = 1.2, ω_e = 1.8, and ω_e = 3.7 for ADR = 0.6 case.

Note from Figure 4 that, at all three frequencies where resonant peaks occur, as marked by i, ii, and iii, there exists two stable periodic solutions. The time histories and the phase paths of the stable periodic oscillations at ω_e = 1.2, ω_e = 1.8, and ω_e = 3.7 are also plotted in Figure 4. It can be noted that at ω_e = 1.2, for both high and low amplitude solutions, the mass oscillates twice as the excitation signal repeats itself once, demonstrating a clear 2:1 super-harmonic behavior (i.e., ω_r:ω_e = 2:1). At ω_e = 1.8 where the primary resonance occurs, the high amplitude solution lags behind the excitation signal by 90 degrees, while the low-amplitude one is approximately in-phase with the excitation. At ω_e = 3.7, two types of periodic solutions exist, where the high amplitude solution corresponds to a 1:2 subharmonic response (i.e., the mass oscillates once in every two excitation cycles). The low amplitude solution shows a 1:1 anti-phase response with the excitation signal.

ii. DR = 1.0 case

The same frequency response analysis is conducted for the ADR = 1.0 case and is shown in Figure 5. It can be noted that, in contrast to the ADR = 0.6 case, the 1:2 subharmonic resonant branch is “attached” to the main branch, that is, only one stable solution exists near the root of the subharmonic branch. Hence this resonant response cannot be “skipped” in a continuous frequency sweep (as shown in Figure 3B). The transition from an isola to an attached response curve is believed to be attributed to the transcritical bifurcation^[52], in other words, the unstable solution between the two stable solutions lowers and eventually merges with the 1:1 harmonic branch as ADR increases.

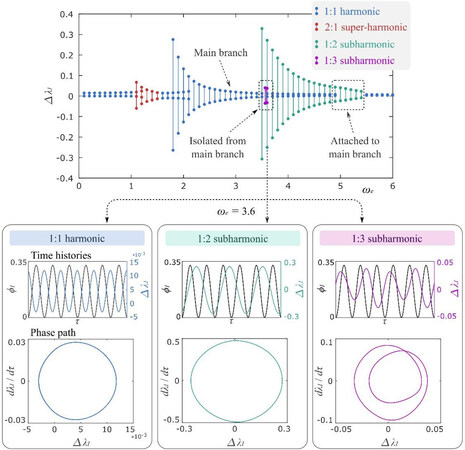
Figure 5. Frequency response, time histories and phase paths of the three stable periodic solutions at ω_e = 3.6 for ADR = 1.0 case.

It is noteworthy that, in the ADR = 1.0 case, a new isola emerges between the 1:1 harmonic and 1:2 subharmonic branches, as is indicated by the purple dots in Figure 5. However, this isola occurs only at a very narrow frequency band from ω_e ≈ 3.65 to 3.75. Note that, at ω_e = 3.7, there exist three stable periodic solutions, and the time history and phase path of each solution are plotted in Figure 5. The solution in purple repeats itself in every three excitation cycles, which correlates to a 1:3 subharmonic response.

iii. Basins of attraction

In the previous study, multiple stable periodic solutions of the DEA system at some excitation frequencies have been demonstrated for both ADR = 0.6 and 1.0 cases. To map the initial conditions that are attracted to the different periodic solutions in the two cases, a point mapping technique^[55] is adopted by dividing the initial condition region of interest into discrete points and numerically computing the steady-state response that each initial condition leads to. By plotting the initial conditions and the corresponding steady-state response, Basins of attraction can be obtained. In this study, the initial displacement and velocity ranges are set as [-0.8, 0.8] and [-1, 1] with a step fixed at 0.08, which lead to a total of 201 × 251 points.

Two cases are considered in this basin of attraction study: (1) ADR = 0.6 and ω_e = 3.7; and (2) ADR = 1.0 and ω_e = 3.6. In the first case, there are two stable periodic responses (i.e., a 1:1 harmonic and 1:2 subharmonic) where the latter one is on the isola, as is demonstrated in Figure 4. In the second case, apart from these two types of periodic orbits, a 1:3 subharmonic response also exists, as is demonstrated in Figure 5.

The basins of attraction for the two cases are plotted in Figure 6A and B, respectively. The black, white and red regions correspond to the periodic oscillations with 1:1 harmonic, 1:2 subharmonic and 1:3 subharmonic responses, respectively. It can be noted that both black and white basins follow a spiral pattern. Also note that the black basin occupies the largest area in both cases, which indicates that, for both cases, the system is more likely to be attracted to a low amplitude 1:1 harmonic response. A more intricate pattern can be found for red basin in Figure 6B and its area is much smaller than the other two basins, meaning it can be more difficult to detect without using the rigorous initial condition search since it is isolated from the main response curve. It is worth noting that, for both cases, there exists a non-negligible possibility to achieve a periodic response on the isolated response curve by adequately perturbing the system.

Figure 6. Basins of attraction for a parametrically forced DEA system with (A) ADR = 0.6, ω_e = 3.7 and (B) ADR = 1.0, ω_e = 3.6. The black, white, and red regions represent the stable periodic solutions with the 1:1 harmonic, 1:2 subharmonic, and 1:3 subharmonic responses, respectively.

Parametric study

In the last section, the frequency response of the DEA system with ADR = 0.6 and ADR = 1.0 were analyzed and isolated response curves were uncovered in both cases. It was noted that the isola observed in the ADR = 0.6 case becomes attached to the main response curve as ADR is increased to 1.0. In this section, an extensive parametric study is conducted to investigate the effects of excitation voltage parameters (ADR and E_a), the damping, and the pre-stretch ratio of the DE membrane on the frequency response of the system. Particular attention is given to the evolution of the isola and its interaction with the main branch.

Effects of excitation parameters

In this subsection, the effects of the excitation parameters (ADR and E_a) on the frequency response of the system are studied. First, the ADR value is varied from 0.2 to 1.0 while keeping E_a as 0.2², and the results are presented in Figure 7. The pre-stretch ratio is set as λ_p = 1.02 and the non-dimensional damping coefficient is . Note that Figure 7 shows the oscillation amplitude as a function of the excitation frequency, defined as the difference between the maximum and minimum values of λ_I in a steady-state periodic oscillation cycle.

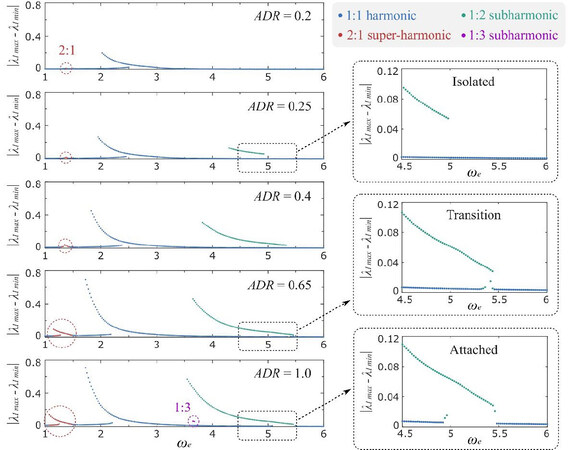
Figure 7. Effects of ADR value on the frequency response of the DEA system. Zoomed in sections show the evolution of the 1:2 subharmonic response curve. λ_p = 1.02, , and E_a = 0.22 are adopted in this study.

As the ADR value increases, both the harmonic forcing amplitude E_b and super-harmonic forcing amplitude E_c in equation 10 increase, which increases the harmonic and super-harmonic resonant amplitudes in Figure 7. It can be noted from Figure 7 that, at a low ADR = 0.2, no subharmonic response can be found in this system, and, as ADR is increased to 0.25, a subharmonic isola emerges and its amplitude grows as ADR increases further. At ADR = 0.65, the isola begins to merge with the main branch, as highlighted in the zoomed-in section. When the ADR value is increased to 1.0, this isolated response curve is firmly attached to the main branch. Meanwhile, a new 1:3 subharmonic isola appears at ADR = 1.0, which is also demonstrated in Figure 5.

In the next study, the ADR value is fixed at 0.6 while varying the E_a and the results are plotted in Figure 8. Increasing the E_a value increases both the AC and DC components of the excitation simultaneously, which causes higher E_b and E_c forcing components; this leads to increases in the amplitudes of both the harmonic and super-harmonic responses. The 1:2 subharmonic response also emerges as E_a increases, first as an isola, before attaching to the main branch as E_a rises further. Note that, as E_a becomes sufficiently high, the displacement from the equilibrium to one end could be greater than 1, which violates the physical constraints of this system (i.e., the mass will collide with the constraint frames). For the case with λ_p = 1.02, , and ADR = 0.6, E_a should be less than 0.25² to avoid collision.

Figure 8. Effects of Ea value on the frequency response of the DEA system. λ_p = 1.02, and ADR = 0.6 are adopted in this study.

Effects of damping

In this subsection, the effects of a physical parameter, i.e., damping coefficient , is investigated with the focus on the excitation frequency range of 3 to 6 where the subharmonic resonant peak occurs. In this study, the ADR, E_a, and λ_p values are set as 0.6, 0.2², and 1.02, respectively, while is increased from 0.02 to 0.1 with an increment of 0.02.

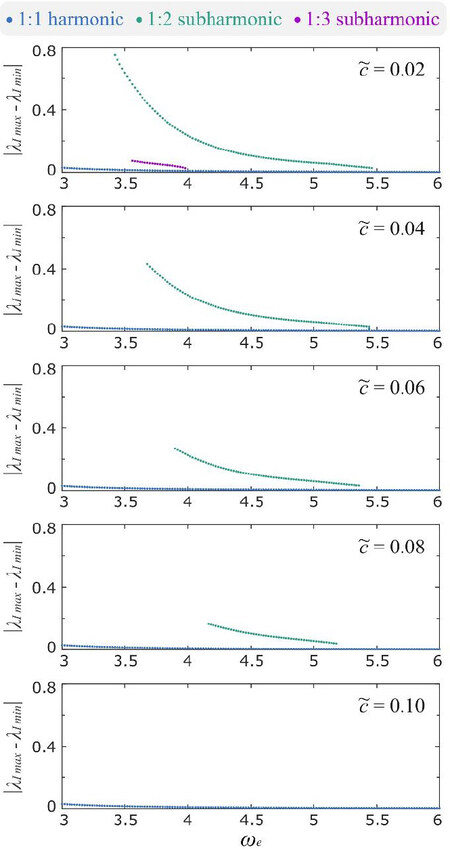
The frequency response of the DEA systems with different damping coefficients are shown in Figure 9. It is worth noting that, for all five cases, the 1:2 subharmonic response curve remains detached from the main curve. As the damping coefficient increases, the size of the isola shrinks and eventually vanishes at . Also note that in the lightest damping case () there exists the 1:3 subharmonic isola, but this isola quickly disappears as becomes higher. The viscous damping in the DE membranes has a clear effect on the development of isolas in this system, for VHB elastomers which have significant viscoelastic properties, the high viscous damping could reduce and even eliminate the isola phenomenon. However, utilizing resonant actuation to optimize the dynamic performance of a DEA system usually requires minimizing the viscous damping in the actuation system, which is one of the main reasons why, in dynamic applications, silicone elastomers are preferable to VHB^[15,16]. It should be noted that silicone DEA systems require comprehensive dynamic analyses to ensure their dynamic behavior is fully understood due to their low viscous damping.

Figure 9. Effects of damping coefficients on the frequency response of the DEA system. λ_p = 1.02, ADR = 0.6, and E_a = 0.22 are adopted in this study.

Effects of pre-stretch

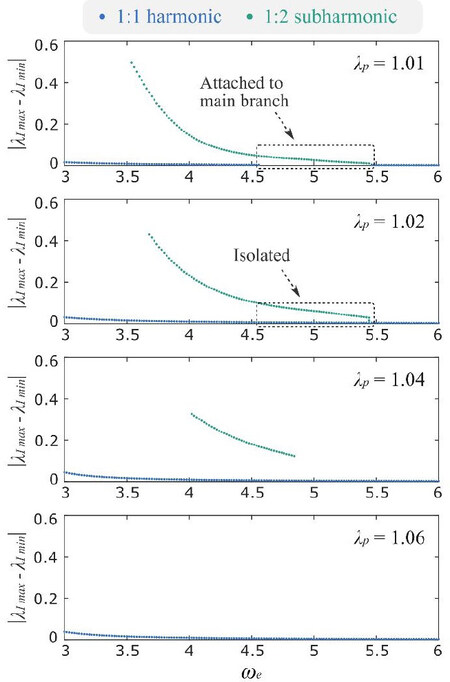
Apart from the damping coefficient, another important physical parameter for the DEA system is the pre-stretch ratio, λ_p. In this study, the pre-stretch ratio is varied from 1.01 to 1.06, while the other parameters are fixed at ADR = 0.6, E_a = 0.2², and . The results of this study are plotted in Figure 10 with a focus on the evolution of the subharmonic response curve. Note from Figure 10 that, at the lowest pre-stretch value of 1.01, the subhramonic response curve is attached to the main branch, and quickly transitions to an isola as λ_p is increased to 1.02. It is noteworthy that increasing λ_p leads to a reduction in the size of the subharmonic response curve, such that the peak amplitude reduces and the bottom of the curve separates further from the main branch. At λ_p = 1.06, the subharmonic curve disappears under the current forcing conditions.

Figure 10. Effects of pre-stretch ratio on the frequency response of the DEA system. ADR = 0.6, E_a = 0.22, and are adopted in this study.

Discussions

The study of the effects of the damping coefficients and the pre-stretch ratios demonstrate that, under the same forcing conditions, by increasing either the damping coefficients or the pre-stretch ratios, the subharmonic response is suppressed and eventually vanishes. However, it cannot be concluded that subharmonic responses, either in isolated or attached form, do not exist in the parametrically forced DEA system when the physical parameters reach those values. For insistence, as is demonstrated in the last subplot in Figures 9 and 10, for (, λ_p = 1.02) and (, λ_p = 1.06) cases, no subharmonic response is observed with the forcing condition of ADR = 0.6 and E_a = 0.2². However, it is found that, by increasing the forcing amplitude, a subharmonic response can be triggered again, as is demonstrated in Figure 11.

Figure 11. Examples showing that, by increasing the forcing amplitude, the vanished subharmonic response can be triggered again. (A) , λ_p = 1.02, and ADR = 0.6. Ea is increased from 0.22 to 0.32. (B) , λ_p = 1.06, and ADR = 0.6. E_a is increased from 0.22 to 0.252.

The structure of the subharmonic response exhibits a complex interaction between the two physical parameters ( and λ_p) and the forcing parameters (ADR and E_a). Note that, by using the control variate technique, the effects of each parameter may be analyzed separately. However, the subharmonic response of this system is due to the interaction between different parameters. As shown in Figure 12, when λ_p reaches 1.2, even though the forcing amplitude is higher (E_a = 0.3²), there is no subharmonic response. Hence a future work that fully investigates the five-dimensional space (ω_e, E_a, ADR, , and λ_p) could enhance the understanding of the isolated resonance responses in the DEA system.

Figure 12. Frequency response of the DEA system with λ_p = 1.2. No subharmonic response can be observed in this example. , ADR = 0.6, and E_a = 0.32 are adopted in this case.